Hamiltonian Dynamics in Haskell

As promised in my hamilton introduction post (published almost exactly one year ago!), I’m going to go over implementing of the hamilton library using

1. DataKinds (with TypeLits) to enforce sizes of vectors and matrices and help guide us write our code
2. Statically-sized linear algebra with hmatrix
3. Automatic differentiation with ad
4. Statically-sized vectors with vector-sized

This post will be a bit heavy in some mathematics and Haskell concepts. The expected audience is intermediate Haskell programmers. Note that this is not a post on dependent types, because dependent types (types that depend on runtime values) are not explicitly used.

The mathematics and physics are “extra” flavor text and could potentially be skipped, but you’ll get the most out of this article if you have basic familiarity with:

1. Basic concepts of multivariable calculus (like partial and total derivatives).
2. Concepts of linear algebra (like dot products, matrix multiplication, and matrix inverses)

No physics knowledge is assumed, but knowing a little bit of first semester physics would help you gain a bit more of an appreciation for the end result!

The hamilton library introduction should be considered a “soft prerequisite” for this post, as it presents motivations, visual demonstrations, and general overviews of the methods presented here!

The Goal

At the end of this, we should be able to have Haskell automatically generate equations of motions for any arbitrary system described in arbitrary coordinate systems, and simulate that system.

Normally, we’d describe a system using particles’ x and y coordinates, but our goal is to be able to describe our particles’ positions using any coordinate system we want (polar, distance-along-a-curved-rail, pendulum-angles, etc.) and have Haskell automatically generate equations of motions and time progressions of those coordinates.

Read my hamilton library introduction for more information and examples!

Hamiltonian Mechanics

As mentioned in the previous post, Hamiltonian mechanics is a re-imagining of dynamics and mechanics (think “the world post-\(F = m a\)”) that not only opened up new doors to solving problems in classical, but also ended up being the right angle of viewing the world to unlock statistical mechanics and thermodynamics, and later even quantum mechanics.

Hamiltonian mechanics lets you parameterize your system’s “position” in arbitrary ways (like the angle of rotation, for pendulum problems) and then posits that the full state of the system exists in something called phase space, and that the system’s dynamics is its motion through phase space that is dictated by the geometry of the Hamiltonian of that phase space.

The system’s Hamiltonian is a \(\mathbb{R}^{2n} \rightarrow \mathbb{R}\) function from a point in \(\mathbb{R}^{2n}\) phase space (where \(n\) is the number of coordinates parameterizing your system) to a scalar in \(\mathbb{R}\). For a time-independent system, the picture of the dynamics is pretty simple: the system moves along the contour lines of the Hamiltonian – the lines of equal “height”.

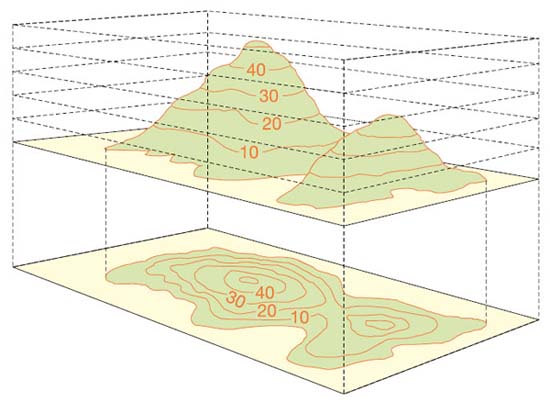
In the example above, if we imagine that phase space is the 2D location, then the Hamiltonian is the mountain. And for a system dropped anywhere on the mountain, its motion would be along the contour lines. For example, if a system started somewhere along the 10 contour line, it would begin to oscillate the entire phase space along the 10 contour line.¹

Every smooth \(\mathbb{R}^{2n} \rightarrow \mathbb{R}\) function on phase space can be used as a Hamiltonian to describe the physics of some system. So, given any “mountain range” on phase space, any “elevation map” or real-valued function on phase space, you can treat it as a description of the dynamics of some physical system.

The trick, then, to using Hamiltonian dynamics to model your system, is:

1. Finding the phase space to describe your system. This can be done based on any continuous parameterization of your system (“generalized coordinates”), like angles of pendulums and so on.

2. Finding the Hamiltonian on that phase space to describe your system.

And then Hamilton’s dynamics will give you the rest! All you do is “follow the contour lines” on that Hamiltonian!

Phase Space

Hamiltonian dynamics are about systems moving around in phase space. It seems that phase space is the “room where it happens”, so to speak, so let’s dig deeper into what it is. Phase space is a \(2n\)-dimensional space parameterized by:

1. All of the current values of the \(n\) parameters (“generalized coordinates”)
2. All of the current “generalized momenta” of those \(n\) parameters

So if you were parameterizing your pendulum system by, say, the angle of the pendulum, then a point in phase space would be the current angle of the pendulum along with the current “generalized momentum” associated with the angle of the pendulum. What exactly is generalized momentum? We’ll go over calculating it eventually, but what does it represent…physically?

The deeper answer involves the underlying Lie algebra of the Lie group associated with the generalized coordinates, but going into that would make this a completely different post. What I can say is that the generalized momenta associated with (“conjugate to”) certain sets of familiar coordinates yield things that we typically call “momenta”:

1. The momentum conjugate to normal Cartesian coordinates is just our normal run-of-the-mill linear momentum (in the \(\mathbf{p} = m \mathbf{v}\)) from first semester physics.

2. The momentum conjugate to the angle \(\theta\) in polar coordinates is angular momentum (\(L = m r^2 \dot{\theta}\)) from first semester physics.

3. The momentum conjugate to the radial coordinate \(r\) in polar coordinates is also just boring old linear momentum \(p_r = m \dot{r}\), which makes sense because purely radial motion is just linear motion.

So, it’s our normal momentum (for linear and polar coordinates) generalized to arbitrary coordinates.

Hamiltonian Dynamics

I’ve explained Hamiltonian dynamics for time-independent Hamiltonians as “follow the contour lines”. If you remember your basic multi-variable calculus course, you’ll know that the line of “steepest ascent” is the gradient. If we call the Hamiltonian \(\mathcal{H}(\mathbf{q},\mathbf{p})\) (where \(\mathbf{q}\) is the vector of positions and \(\mathbf{p}\) is the vector of momenta), then the direction of steepest ascent is

\[ \left \langle \frac{\partial}{\partial \mathbf{q}} \mathcal{H}(\mathbf{q},\mathbf{p}), \frac{\partial}{\partial \mathbf{p}} \mathcal{H}(\mathbf{q},\mathbf{p}) \right \rangle \]

But we want to move along the contour lines…and these are the lines perpendicular to the direction of steepest descent. The vector perpendicular to \(\langle x, y \rangle\) is \(\langle y, -x \rangle\),² so we just derived the actual Hamiltonian equations of motion: just move in the direction perpendicular to the steepest ascent! That is, to have things move on contour lines, \(\dot{q}\) and \(\dot{p}_q\) should be:

\[ \begin{aligned} \dot{q} & = \frac{\partial}{\partial p_q} \mathcal{H}(\mathbf{q},\mathbf{p}) \\ \dot{p}_q & = - \frac{\partial}{\partial q} \mathcal{H}(\mathbf{q},\mathbf{p}) \end{aligned} \]

This is a conclusion with one generalized coordinate \(q\), but we can generalize this to systems with multiple coordinates as well, as long as this holds for every \(q\) and the momentum conjugate to it (\(p_q\)). (For the rest of this post, \(\mathbf{q}\) refers to the vector of coordinates, \(q\) refers to a single specific coordinate, and \(p_q\) refers to the momentum conjugate to that coordinate).

Essentially, these give you “updating functions” for \(q\) and \(p_q\) – given \(\mathcal{H}(\mathbf{q},\mathbf{p})\), you have a way to “update” the particle’s position in phase space. Just take the partial derivatives of \(\mathcal{H}\) at every step in time! To update \(q\), nudge it by \(\frac{\partial}{\partial p_q} \mathcal{H}(\mathbf{q},\mathbf{p})\). To update \(p_q\), nudge it by \(-\frac{\partial}{\partial q} \mathcal{H}(\mathbf{q},\mathbf{p})\)!

This picture is appealing to me in a visceral way because it sort of seems like the system is “surfing” along the Hamiltonian’s contour lines. It’s being “pushed” faster when the Hamiltonian is steeper, and slower when it’s more shallow. I can apply all my intuition as a surfer³ to Hamiltonian mechanics!

Hamiltonian Dynamics and Physical Systems

Earlier I mentioned that the two steps for applying Hamiltonian mechanics to your system was figuring out your system’s conjugate momenta and the appropriate Hamiltonian. To explain this, I’m going to make a couple of simplifying assumptions that make the job easier for the purposes of this article:

1. Your coordinates and potential energy are time-independent.
2. Your potential energy function only depends on positions, and not velocities. (So nothing like friction or wind resistance or magnetic field vector potentials)

With these assumptions, I’m going to skip over discussing the Lagrangian of the system, which is the traditional way to do this. You can think of this section as me presenting derived conclusions and skipping the derivations.

Conjugate Momenta

For systems with velocity-independent potential energies, it can be shown that the momentum conjugate to coordinate \(q\) is

\[ p_q = \frac{\partial}{\partial \dot{q}} KE(\mathbf{q}, \dot{\mathbf{q}}) \]

Where \(KE(\mathbf{q},\dot{\mathbf{q}})\) is the kinetic energy of the system, which is a function on the coordinates \(\mathbf{q}\) and their rates of change, \(\dot{\mathbf{q}}\). For example, for normal Cartesian coordinates in one dimension, \(KE(x, \dot{x}) = \frac{1}{2} m \dot{x}^2\). So the momentum conjugate to \(x\) is:

\[ p_x = \frac{\partial}{\partial \dot{x}} \left[ \frac{1}{2} m \dot{x}^2 \right] = m \dot{x} \]

Just linear momentum, like I claimed before.

Let’s generalize this to arbitrary coordinates. In general, for Cartesian coordinates, the kinetic energy will always be

\[ KE(\mathbf{x}, \dot{\mathbf{x}}) = \frac{1}{2} \left[ m_1 \dot{x}_1^2 + m_2 \dot{x}_2^2 + m_3 \dot{x}_3^2 + \dots \right] \]

Where \(m\) is the inertia associated with each coordinate…for example, if \(\langle x_1, x_2 \rangle\) describes the location of an object of mass \(m\), then \(m_1 = m_2 = m\).

To give us nice notation and make things more convenient, we’ll write this as a quadratic form over an inertia matrix:

\[ KE(\dot{\mathbf{x}}) = \frac{1}{2} \dot{\mathbf{x}}^T \hat{M} \dot{\mathbf{x}} \]

Where \(\hat{M}\) is the diagonal matrix whose entries are the masses of each coordinate, and \(\dot{\mathbf{x}}\) is the column vector of all of the (Cartesian) coordinates, \(\left[ \dot{x}_1\, \dot{x}_2\, \dot{x}_3\, \dots \right]^T\).

Now! How to generalize this to arbitrary coordinates? Well, if we have \(n\) generalized coordinates \(\mathbf{q}\) mapping to \(m\)-dimensional Cartesian coordinates, we can specify them as \(\mathbf{x} = f(\mathbf{q})\), where \(f : \mathbb{R}^n \rightarrow \mathbb{R}^m\), taking the vector of generalized coordinates and returning a vector for the position in Cartesian space. For example, for polar coordinates, \(f(r, \theta) = \left \langle r \cos(\theta), r \sin(\theta) \right \rangle\), because, for polar coordinates, \(x = r \cos(\theta)\) and \(y = r \sin(\theta)\).

So we can get \(\mathbf{x}\) from \(\mathbf{q}\) with \(f\), but how can we get \(\dot{\mathbf{x}}\), the vector of rate of changes? Well, if \(x_1 = f_1(q_1, q_2, q_3 \dots)\), then the \(\dot{x}_1\) is the total derivative of \(x_1\) with respect to time:

\[ \dot{x}_1 = \frac{\partial f_1}{\partial q_1} \dot{q}_1 + \frac{\partial f_1}{\partial q_2} \dot{q}_2 + \frac{\partial f_1}{\partial q_3} \dot{q}_3 + \dots \]

Or, in short:

\[ \dot{x}_i = \sum_{j = 1}^n \frac{\partial f_i}{\partial q_j} \dot{q}_j \]

But, hey, this looks a lot like a matrix-vector multiplication! If we make \(\hat{J}_f\), an \(m \times n\) matrix of partial derivatives of \(f\) (\(\hat{J}_{fij} = \frac{\partial f_i}{\partial q_j}\)) at a given point (typically called the Jacobian matrix of f), then we have a nice expression for \(\dot{\mathbf{x}}\):

\[ \dot{\mathbf{x}} = \hat{J}_f \dot{\mathbf{q}} \]

And we can plug it in (remembering that \((A B)^T = B^T A^T\)) to our kinetic energy equation to get:

\[ KE(\mathbf{q},\dot{\mathbf{q}}) = \frac{1}{2} \dot{\mathbf{q}}^T \hat{J}_f^T \hat{M} \hat{J}_f \dot{\mathbf{q}} \]

And for the final step, we differentiate with respect to the \(\dot{q}\)s (which is just the gradient \(\nabla_{\dot{\mathbf{q}}}\)) to get \(\mathbf{p}\), the vector of conjugate momenta:

\[ \mathbf{p} = \nabla_{\dot{\mathbf{q}}} \left[ \frac{1}{2} \dot{\mathbf{q}}^T \hat{J}_f^T \hat{M} \hat{J}_f \dot{\mathbf{q}} \right] = \hat{J}_f^T \hat{M} \hat{J}_f \dot{\mathbf{q}} \]

Now, we’re going to be using \(\hat{J}_f^T \hat{M} \hat{J}_f\) a lot, so let’s give it a name, \(\hat{K}\). \(\hat{K}\) represents some sort of coordinate-aware inertia term for our system. If the masses are all positive and \(\hat{J}_f\) is full-rank⁴, then \(\hat{K}\) is a symmetric, positive-definite, invertible matrix (by construction). It’s important to also remember that it’s an explicit function of \(\mathbf{q}\), because \(\hat{J}_f\) is a matrix of partial derivatives at a given \(\mathbf{q}\). We now have a simple expression for the vector of conjugate momenta (\(\mathbf{p} = \hat{K} \dot{\mathbf{q}}\)), and also for kinetic energy (\(KE = \frac{1}{2} \dot{\mathbf{q}}^T \hat{K} \dot{\mathbf{q}}\)).

It’s going to be important for us to also be able to go backwards (to get \(\dot{\mathbf{q}}\) from \(\mathbf{p}\)). Luckily, because we wrote the whole thing as a matrix operation, going backwards is easy – just take the matrix inverse, which we know exists!

\[ \dot{\mathbf{q}} = \hat{K}^{-1} \mathbf{p} \]

The power of linear algebra!

Hamiltonians of Physical Systems

Ok, that’s step one. How about step two – finding the Hamiltonian for your system?

The real Hamiltonian is actually the Poisson bracket of the system’s Lagrangian, but I did some of the work for you for the case of time-independent coordinates where the potential energy depends only on positions (so, no friction, wind resistance, time, etc.). In such a case, the Hamiltonian of a system is precisely the system’s total mechanical energy, or its kinetic energy plus the potential energy:

\[ \mathcal{H}(\mathbf{q},\mathbf{p}) = KE(\mathbf{q},\mathbf{p}) + PE(\mathbf{q}) \]

Which makes a lot of intuitive sense, because you might recall that total mechanical energy is always conserved for certain types of systems. Incidentally, Hamiltonian dynamics makes sure that the value of the system’s Hamiltonian stays the same (because it moves along contour lines). So, the system’s Hamiltonian always stays the same, and so its total mechanical energy stays the same, as well! Energy is conserved because the Hamiltonian stays the same!

Anyway, we want to build our system’s Hamiltonian from properties of the coordinate system, so plugging in our expression for \(KE\), we get \(\mathcal{H}(\mathbf{q},\dot{\mathbf{q}}) = \frac{1}{2} \dot{\mathbf{q}}^T \hat{K} \dot{\mathbf{q}} + PE(\mathbf{q})\).

Oh, but oops, the Hamiltonian has to be a function of \(\mathbf{p}\), not of \(\dot{\mathbf{q}}\). Let’s remember that \(\dot{\mathbf{q}} = \hat{K}^{-1} \mathbf{p}\) and find the final form of our Hamiltonian (after a bit of simplification, remembering that the inverse of a symmetric matrix is also symmetric):

\[ \mathcal{H}(\mathbf{q},\mathbf{p}) = \frac{1}{2} \mathbf{p}^T \hat{K}^{-1} \mathbf{p} + PE(\mathbf{q}) \]

Hamiltonian Equations

We got our Hamiltonian! Now just to find our updating functions (the partial derivatives of the Hamiltonian), and we’re done with the math.

Because we are assuming the case (with loss of generality) \(PE\) doesn’t depend on \(\mathbf{p}\), the partial derivatives of \(\mathcal{H}\) with respect to \(\mathbf{p}\) is:

\[ \nabla_{\mathbf{p}} \mathcal{H}(\mathbf{q},\mathbf{p}) = \hat{K}^{-1} \mathbf{p} \]

We already can calculate \(\hat{K}^{-1}\), so this wound up being easy peasy. But finding the partial derivatives with respect to \(\mathbf{q}\) is a little trickier. The gradient is a linear operator, so we can break that down to just finding the gradient of the \(KE\) term \(\frac{1}{2} \mathbf{p}^T \hat{K}^{-1} \mathbf{p}\). Because \(\mathbf{p}\) is an independent input to \(\mathcal{H}\), we can just look at the gradient of \(\hat{K}^{-1}\). We can simplify that even more by realizing that for any invertible matrix \(A\), \(\frac{\partial}{\partial q} A^{-1} = - A^{-1} \left[ \frac{\partial}{\partial q} A \right] A^{-1}\), so now we just need to find the partial derivatives of \(\hat{K}\), or \(\hat{J}_f^T \hat{M} \hat{J}_f\). \(\hat{M}\) is a constant term, so, using the good ol’ product rule over \(\hat{J}_f^T\) and \(\hat{J}_f\), we see that, after some simplification:

\[ \frac{\partial}{\partial q_i} \left[ \hat{J}_f^T \hat{M} \hat{J}_f \right] = 2 \hat{J}_f^T \hat{M} \left[ \frac{\partial}{\partial q_i} \hat{J}_f \right] \]

\(\frac{\partial}{\partial q_i} \hat{J}_f\) (an \(m \times n\) matrix, like \(\hat{J}_f\)) represents the second derivatives of \(f\) – the derivative (with respect to \(q_i\)) of the derivatives.

The collection of “second-order derivatives of \(f\)” is known as the Hessian Tensor (a vector-valued generalization of the Hessian matrix), which we will denote as \(\hat{H}_f\).⁵ We can write this in a nicer way by abusing matrix multiplication notation to get

\[ \nabla_{\mathbf{q}} \left[ \hat{J}_f^T \hat{M} \hat{J}_f \right] = 2 \hat{J}_f^T \hat{M} \hat{H}_f \]

if we use \(\hat{H}_f\) as an \(n \times m \times n\) tensor, whose \(n\) components are the each the \(m \times n\) matrices corresponding to \(\frac{\partial}{\partial q_i} \hat{J}_f\)

And with that, we have our final expression for \(\nabla_{\mathbf{q}} \mathcal{H}(\mathbf{q},\mathbf{p})\):

\[ \frac{\partial}{\partial q_i} \mathcal{H}(\mathbf{q},\mathbf{p}) = - \mathbf{p}^T \hat{K}^{-1} \hat{J}_f^T \hat{M} \left[ \frac{\partial}{\partial q_i} \hat{J}_f \right] \hat{K}^{-1} \mathbf{p} + \nabla_{\mathbf{q}} PE(\mathbf{q}) \]

Or, to use our abuse of notation:

\[ \nabla_{\mathbf{q}} \mathcal{H}(\mathbf{q},\mathbf{p}) = - \mathbf{p}^T \hat{K}^{-1} \hat{J}_f^T \hat{M} \hat{H}_f \hat{K}^{-1} \mathbf{p} + \nabla_{\mathbf{q}} PE(\mathbf{q}) \]

And, finally, we have everything we need – we can now construct our equations of motion! To progress through phase space (\(\langle \mathbf{q}, \mathbf{p}\rangle\)):

\[ \begin{aligned} \dot{\mathbf{q}} & = \nabla_{\mathbf{p_q}} \mathcal{H}(\mathbf{q},\mathbf{p}) && = \hat{K}^{-1} \mathbf{p} \\ \dot{\mathbf{p}} & = - \nabla_{\mathbf{q}} \mathcal{H}(\mathbf{q},\mathbf{p}) && = \mathbf{p}^T \hat{K}^{-1} \hat{J}_f^T \hat{M} \hat{H}_f \hat{K}^{-1} \mathbf{p} - \nabla_{\mathbf{q}} PE(\mathbf{q}) \end{aligned} \]

That’s it. We’re done. Have a nice day, thanks for reading!

The Haskell

Just kidding, now it’s time for the fun stuff :)

Our final goal is to be able to simulate a system of discrete particles through arbitrary generalized coordinates.

To simplify the math, we always assume that, whatever generalized coordinates you are using (\(\mathbb{R}^n\)), your system “actually” exists in some real flat Cartesian coordinate system (\(\mathbb{R}^m\)). This allows us to take advantage of all of that math we derived in the previous section.

So, in order to fully describe the system, we need:

1. Each of their masses (or inertias) in their underlying \(m\) Cartesian coordinates, which we’ll call \(\mathbf{m}\).
2. A function \(f : \mathbb{R}^n \rightarrow \mathbb{R}^m\) to convert the generalized coordinates (\(\mathbb{R^n}\)) to Cartesian coordinates (\(\mathbb{R}^m\))
3. The potential energy function \(U : \mathbb{R}^n \rightarrow \mathbb{R}\) in the generalized coordinates (\(\mathbb{R^n}\))

From these alone, we can derive the equations of motion for the particles in phase space as a system of first-order ODEs using the process described above. Then, given an initial phase space position, we can do numeric integration to simulate our system’s motion through phase space. To “surf the Hamiltonian waves in phase space”, so to speak.

But, to be explicit, we also are going to need some derivatives for these functions/vectors, too. If you’ve been following along, the full enumeration of functions and vectors we need is:

\[ \begin{aligned} \mathbf{m} & : \mathbb{R}^m \\ f & : \mathbb{R}^n \rightarrow \mathbb{R}^m \\ \hat{J}_f & : \mathbb{R}^n \rightarrow \mathbb{R}^{m \times n} \\ \hat{H}_f & : \mathbb{R}^n \rightarrow \mathbb{R}^{n \times m \times n} \\ U & : \mathbb{R}^n \rightarrow \mathbb{R} \\ \nabla_{\mathbf{q}} U & : \mathbb{R}^n \rightarrow \mathbb{R}^n \end{aligned} \]

But, as we’ll see, with libraries like ad in Haskell, we can really just ask the user for \(\mathbf{m}\), \(f\), and \(U\) – all of the derivatives can be computed automatically.

Our Data Structures

We can couple together all of these functions in a data type that fully describes the physics of our systems (the “shape” of the Hamiltonian):

-- source: https://github.com/mstksg/inCode/tree/master/code-samples/hamilton1/Hamilton.hs#L25-L32

data System m n = System
    { sysInertia       :: R m                         -- ^ 'm' vector
    , sysCoords        :: R n -> R m                  -- ^ f
    , sysJacobian      :: R n -> L m n                -- ^ J_f
    , sysHessian       :: R n -> V.Vector n (L m n)   -- ^ H_f
    , sysPotential     :: R n -> Double               -- ^ U
    , sysPotentialGrad :: R n -> R n                  -- ^ grad U
    }

R n and L m n are from the hmatrix library; an R n represents an n-vector (For example, an R 4 is a 4-vector), and an L m n represents an m x n matrix (For example, an L 5 3 is a 5x3 matrix).

A System m n will describe a system parameterized by n generalized coordinates, taking place in an underlying m-dimensional Cartesian space.

It’ll also be convenient to have a data type to describe the state of our system in terms of its generalized positions (\(\mathbf{q}\)) and generalized velocities (the rates of changes of these positions, \(\dot{\mathbf{q}}\)), which is sometimes called “configuration space”:

-- source: https://github.com/mstksg/inCode/tree/master/code-samples/hamilton1/Hamilton.hs#L35-L39

data Config n = Config
    { confPositions  :: R n
    , confVelocities :: R n
    }
  deriving Show

And, more importantly, remember that Hamiltonian dynamics is all about surfing around on that phase space (generalized positions \(\mathbf{q}\) and their conjugate momenta, \(\mathbf{p_q}\)). So let’s make a type to describe the state of our system in phase space:

-- source: https://github.com/mstksg/inCode/tree/master/code-samples/hamilton1/Hamilton.hs#L42-L46

data Phase n = Phase
    { phasePositions :: R n
    , phaseMomenta   :: R n
    }
  deriving Show

Getting comfortable with our data types

First of all, assuming we can construct a System in a sound way, let’s imagine some useful functions.

We can write a function underlyingPosition, which allows you to give a position in generalized coordinates, and returns the position in the “underlying coordinate system”:

-- source: https://github.com/mstksg/inCode/tree/master/code-samples/hamilton1/Hamilton.hs#L51-L55

underlyingPosition
    :: System m n
    -> R n
    -> R m
underlyingPosition = sysCoords

Note that the types in our function helps us know exactly what the function is doing — and also helps us implement it correctly. If we have a System in n dimensions, over an underlying m-dimensional Cartesian space, then we would need to convert an R n (an n-dimensional vector of all of the positions) into an R m (a vector in the underlying Cartesian space).

Simple enough, but let’s maybe try to calculate something more complicated: the momenta of a system, given its positions and velocities (configuration).

We remember that we have a nice formula for that, up above:

\[ \mathbf{p} = \hat{J}_f^T \hat{M} \hat{J}_f \dot{\mathbf{q}} \]

We can translate that directly into Haskell code:

-- source: https://github.com/mstksg/inCode/tree/master/code-samples/hamilton1/Hamilton.hs#L59-L67

momenta
    :: (KnownNat n, KnownNat m)
    => System m n
    -> Config n
    -> R n
momenta s (Config q v) = tr j #> mHat #> j #> v
  where
    j    = sysJacobian s q
    mHat = diag (sysInertia s)

Note that, because our vectors have their size indexed in their type, this is pretty simple to write and ensure that the shapes “line up”. In fact, GHC can even help you write this function by telling you what values can go in what locations. Being able to get rid of a large class of bugs and clean up your implementation space is nice, too!

(Note that hmatrix requires a KnownNat constraint on the size parameters of our vectors for some functions, so we add this as a constraint on our end.)

With this, we can write a function to convert any state in configuration space to its coordinates in phase space:

-- source: https://github.com/mstksg/inCode/tree/master/code-samples/hamilton1/Hamilton.hs#L70-L75

toPhase
    :: (KnownNat n, KnownNat m)
    => System m n
    -> Config n
    -> Phase n
toPhase s c = Phase (confPositions c) (momenta s c)

This function is important, because “configuration space” is how we actually directly observe our system – in terms of positions and velocities, and not in terms of positions and momenta (and sometimes conjugate momenta might not even have meaningful physical interpretations). So, having toPhase lets us “initialize” our system in terms of direct observables, and then convert it to its phase space representation, which is something that Hamiltonian mechanics can work with.

Automatic Differentiation

Now, creating a System “from scratch” is not much fun, because you would have to manually differentiate your coordinate systems and potentials to generate your Jacobians and gradients.

Here’s where the magic comes in – we can have Haskell generate our Jacobians and gradients automatically, using the amazing ad library! We can just use the appropriately named grad, jacobian, and hessianF functions.

Quick Intro to AD

At the simplest level, if we have a function from some number to some other number, we can use diff to get its derivative:

myFunc      :: RealFloat a => a -> a
diff myFunc :: RealFloat a => a -> a

If we have a function from a sized vector to a scalar, we can use grad to get its gradient:

-- import qualified Data.Vector.Sized as V

myFunc      :: RealFloat a => V.Vector n a -> a
grad myFunc :: RealFloat a => V.Vector n a -> V.Vector n a

Where each of the components in the resulting vector corresponds to the rate of change of the output according to variations in that component.

We’re using statically sized vector type from the vector-sized package (in the Data.Vector.Sized module), where V.Vector n a is a n-vector of as – for example, a V.Vector 3 Double is a vector of 3 Doubles.

We have to use Vector (instead of R, from hmatrix) because automatic differentiation for gradients requires some Functor to work. An R 5 is essentially a V.Vector 5 Double, except the latter can contain other, non-Double things – and therefore can be used by ad to do its magic.

If we have a function from a sized vector to a (differently) sized vector, we can use the jacobian function to get its jacobian!

myFunc          :: RealFloat a => V.Vector n a -> V.Vector m a
jacobian myFunc :: RealFloat a => V.Vector n a -> V.Vector m (V.Vector n a)

Again note the usage of sized vector types, and the fact that our \(m \times n\) matrix is represented by a m-vector of n-vectors.

Finally, we can get our Hessian Tensor by using hessianF:⁶

myFunc
    :: RealFloat a => V.Vector n a -> V.Vector m a
hessianF myFunc
    :: RealFloat a => V.Vector n a -> V.Vector m (V.Vector n (V.Vector n a))

Conversion between vector-sized and hmatrix

Just a small hiccup — the ad libraries requires our vectors to be Functors, but R and L from hmatrix are not your typical capital-F Functor instances in Haskell. We just need to do some manual conversion using the hmatrix-vector-sized library.

This gives functions like:

-- import qualified Data.Vector.Sorable.Sized as VS
gvecR :: V.Vector n Double  -> R n
grVec :: R n                -> V.Vector n Double
rowsL :: V.Vector m (R n)   -> L m n
lRows :: L m n              -> V.Vector m (R n)

to allow us to convert back and forth.

Also, even though ad gives our Hessian as an \(m \times n \times n\) tensor, we really want it as a n-vector of \(m \times n\) matrices – that’s how we interpreted it in our original math. So we just need to write an function to convert what ad gives us to the form we expect. Just a minor reshuffling:

-- source: https://github.com/mstksg/inCode/tree/master/code-samples/hamilton1/Hamilton.hs#L78-L82

tr2 :: (KnownNat m, KnownNat n)
    => V.Vector m (L n n)
    -> V.Vector n (L m n)
tr2 = fmap rowsL . traverse lRows
{-# INLINE tr2 #-}

We also would need to have a function converting a vector of vectors into a matrix:

-- source: https://github.com/mstksg/inCode/tree/master/code-samples/hamilton1/Hamilton.hs#L85-L90

vec2l
    :: KnownNat n
    => V.Vector m (V.Vector n Double)
    -> L m n
vec2l = rowsL . fmap gvecR
{-# INLINE vec2l #-}

Using AD to Auto-Derive Systems

Now to make a System using just the mass vector, the coordinate conversion function, and the potential energy function:

-- source: https://github.com/mstksg/inCode/tree/master/code-samples/hamilton1/Hamilton.hs#L94-L108

mkSystem
    :: (KnownNat m, KnownNat n)
    => R m
    -> (forall a. RealFloat a => V.Vector n a -> V.Vector m a)
    -> (forall a. RealFloat a => V.Vector n a -> a)
    -> System m n
mkSystem m f u = System
                    -- < convert from      | actual thing | convert to >
    { sysInertia       =                     m
    , sysCoords        =        gvecR      . f            . grVec
    , sysJacobian      = tr   . vec2l      . jacobianT f  . grVec
    , sysHessian       = tr2  . fmap vec2l . hessianF f   . grVec
    , sysPotential     =                     u            . grVec
    , sysPotentialGrad =        gvecR      . grad u       . grVec
    }

Now, I hesitate to call this “trivial”…but, I think it really is a straightforward direct translation of the definitions, minus some boilerplate conversions back and forth between vector using vecR, rVec, etc.!

1. The vector of masses is just m
2. The coordinate function is just f
3. The Jacobian of the coordinate function is just jacobian f
4. The Hessian Tensor of the coordinate function is just hessianF f
5. The potential energy function is just u
6. The gradient of the potential energy function is just grad u

The ad library automatically generated all of these for us and created a perfectly well-formed System with all of its gradients and Jacobians and Hessians by giving only the coordinate function and the potential energy function, and in such a clean and concise way!

Equations of Motion

At this point, we’re ready to write our final equations of motion, which we found to be given by:

\[ \begin{aligned} \dot{\mathbf{q}} & = \hat{K}^{-1} \mathbf{p} \\ \dot{\mathbf{p}} & = \mathbf{p}^T \hat{K}^{-1} \hat{J}_f^T \hat{M} \left[ \nabla_{\mathbf{q}} \hat{J}_f \right] \hat{K}^{-1} \mathbf{p} - \nabla_{\mathbf{q}} PE(\mathbf{q}) \end{aligned} \]

These equations aren’t particularly beautiful, but it’s straightforward to translate them into Haskell (using \(\hat{K} = \hat{J}_f^T \hat{M} \hat{J}_f\)):

-- source: https://github.com/mstksg/inCode/tree/master/code-samples/hamilton1/Hamilton.hs#L112-L129

hamilEqns
    :: (KnownNat n, KnownNat m)
    => System m n
    -> Phase n
    -> (R n, R n)       -- dq/dt and dp/dt
hamilEqns s (Phase q p) = (dqdt, dpdt)
  where
    j       = sysJacobian s q
    trj     = tr j
    mHat    = diag (sysInertia s)
    kHat    = trj `mul` mHat `mul` j
    kHatInv = inv kHat
    dqdt    = kHatInv #> p
    dpdt    = gvecR bigUglyThing - sysPotentialGrad s q
      where
        bigUglyThing =
          fmap (\j2 -> -p <.> kHatInv #> trj #> mHat #> j2 #> kHatInv #> p)
               (sysHessian s q)

Of course, there is no way to get around the big ugly math term in \(\dot{p}_q\), but at least it is a direct reading of the math!

But!! I’d much rather write this scary Haskell than that scary math, because ghc typechecks our math! When writing out those equations, we really had no idea if we were writing it correctly, and if the matrix and vector and tensor dimensions line up. If it even made sense to multiply and transpose the quantities we had.

However, when writing hamilEqns, we let GHC hold our hand for us. If any of our math is wrong, GHC will verify it for us! If any dimensions don’t match up, or any transpositions don’t make sense, we’ll know immediately. And if we’re ever lost, we can leave a typed hole – then GHC will tell you all of the values in scope that can fit in that hole! Even if you don’t completely understand the math, this helps you implement it in a somewhat confident way.

It’s admittedly difficult to convey how helpful these sized vector types are without working through trying to implement them yourself, so feel free to give it a try when you get the chance! :D

Numerical Integration

The result of hamilEqns gives the rate of change of the components of our Phase n. The rest of the processes then is just to “step” Phase n. Gradually update it, following these rate of changes!

This process is known as numerical integration. The “best” way to do it is quite a big field, so for this article we’re going to be using the extremely extremely simple Euler method to progress our system through time.

Disclaimer – The Euler method is typically a very very bad choice for numerical integration (even though, as popularized in the movie Hidden Figures, it was good enough to send humans to space?). We are just choosing it for this article because it’s very simple, conceptually!

The basic idea is that you pick a time-step, \(\Delta t\), and update each coordinate as:

\[ x(t + \Delta t) = x(t) + \dot{x}(t) \Delta t \]

Which makes sense visually if we imagine \(\dot{x}\) as the “slope” of \(x\) – it just means to follow the slope another \(\Delta t\) steps. If the slope stays constant, this method is perfectly accurate. The inaccuracy, of course, happens when the slope changes drastically within that \(\Delta t\) (and also from the fact that small errors cause errors in the new calculations of \(\dot{x}\), and so compound over time)

You can understand this symbolically, as well, by remembering that the derivative can be approximated by \(\dot{x}(t) \approx \frac{x(t + \Delta t) - x(t)}{\Delta t}\) for small \(\Delta t\), and so we can do a little bit of symbolic manipulation to get \(x(t + \Delta t) \approx \dot{x}(t) \Delta t + x(t)\).

We can directly translate this into Haskell: (using konst :: KnownNat n => Double -> R n, making a constant vector, and *, the component-wise product of two vectors)

-- source: https://github.com/mstksg/inCode/tree/master/code-samples/hamilton1/Hamilton.hs#L132-L140

stepEuler
    :: (KnownNat n, KnownNat m)
    => System m n       -- ^ the system
    -> Double           -- ^ dt
    -> Phase n          -- ^ q(t) and p(t)
    -> Phase n          -- ^ q(t + dt) and p(t + dt)
stepEuler s dt ph@(Phase q p) = Phase (q + konst dt * dq) (p + konst dt * dp)
  where
    (dq, dp) = hamilEqns s ph

And repeatedly evolve this system as a lazy list:

-- source: https://github.com/mstksg/inCode/tree/master/code-samples/hamilton1/Hamilton.hs#L143-L151

runSystem
    :: (KnownNat n, KnownNat m)
    => System m n       -- ^ the system
    -> Double           -- ^ dt
    -> Phase n          -- ^ initial phase
    -> [Phase n]        -- ^ progression of the system using Euler integration
runSystem s dt = go
  where
    go p0 = p0 : go (stepEuler s dt p0)

Running with it

And…that’s it! Granted, in real life, we would be using a less naive integration method, but this is essentially the entire process!

Let’s generate the boring system, a 5kg particle in 2D Cartesian Coordinates under gravity –

-- source: https://github.com/mstksg/inCode/tree/master/code-samples/hamilton1/Hamilton.hs#L154-L160

simpleSystem :: System 2 2
simpleSystem = mkSystem (vec2 5 5) id pot
  where
    -- potential energy of a gravity field
    -- U(x,y) = 9.8 * y
    pot :: RealFloat a => V.Vector 2 a -> a
    pot xy = 9.8 * (xy `V.index` 1)

If we initialize the particle at position \(\mathbf{q}_0 = \langle 0, 0 \rangle\) and velocity \(\mathbf{v}_0 = \langle 1, 3 \rangle\) (that is, \(v_x = 1\) and \(v_y = 3\)), we should see something that travels at a constant velocity in x and something that starts moving “upwards” (in positive y) and eventually reaches a peak and moves downwards.

We can make our initial configuration:

-- source: https://github.com/mstksg/inCode/tree/master/code-samples/hamilton1/Hamilton.hs#L164-L168

simpleConfig0 :: Config 2
simpleConfig0 = Config
    { confPositions  = vec2 0 0
    , confVelocities = vec2 1 3
    }

And then…let it run!

-- source: https://github.com/mstksg/inCode/tree/master/code-samples/hamilton1/Hamilton.hs#L170-L174

simpleMain :: IO ()
simpleMain =
    mapM_ (disp 2 . phasePositions)  -- position with 2 digits of precision
  . take 25                          -- 25 steps
  $ runSystem simpleSystem 0.1 (toPhase simpleSystem simpleConfig0)

We get:

ghci> :l Hamilton.hs
ghci> simpleMain
0     0
0.10  0.30
0.20  0.58
0.30  0.84
0.40  1.08
0.50  1.30
0.60  1.51
0.70  1.69
0.80  1.85
0.90  1.99
1.00  2.12
1.10  2.22
1.20  2.31
1.30  2.37
1.40  2.42
1.50  2.44
1.60  2.45
1.70  2.43
1.80  2.40
1.90  2.35
2.00  2.28
2.10  2.18
2.20  2.07
2.30  1.94
2.40  1.79

Exactly what we’d expect! The x positions increase steadily, and the y positions increase, slow down, and start decreasing.

We can try a slightly more complicated example that validates (and justifies) all of the work we’ve done – let’s simulate a simple pendulum. The state of a pendulum is characterized by one coordinate \(\theta\), which refers to the angular (clockwise) from the equilibrium “hanging straight down” position. \(\theta = 0\) corresponds to 6 o’ clock, \(\theta = \pi/2\) corresponds to 9 o’ clock, \(\theta = - \pi / 2\) corresponds to 3 o’ clock, etc. For a pendulum of length \(l\), we can translate that as \(\langle x, y \rangle = \langle - l sin(\theta), - l cos(\theta) \rangle\).

Let’s set up that system! We’ll put it under normal gravity potential, again (\(U(x,y) = 9.8 y\)). Our initial position \(\theta_0\) will be at equilibrium, and our initial angular velocity \(v_{\theta 0}\) will be 0.1 radians/sec (clockwise), as we try to induce harmonic motion:

-- source: https://github.com/mstksg/inCode/tree/master/code-samples/hamilton1/Hamilton.hs#L179-L204

pendulum :: System 2 1
pendulum = mkSystem (vec2 5 5) coords pot      -- 5kg particle
  where
    -- <x,y> = <-0.5 sin(theta), -0.5 cos(theta)>
    -- pendulum of length 0.25
    coords :: RealFloat a => V.Vector 1 a -> V.Vector 2 a
    coords (V.head->theta) = V.fromTuple (- 0.25 * sin theta, - 0.25 * cos theta)
    -- potential energy of gravity field
    -- U(x,y) = 9.8 * y
    pot :: RealFloat a => V.Vector 1 a -> a
    pot q = 9.8 * (coords q `V.index` 1)

pendulumConfig0 :: Config 1
pendulumConfig0 = Config
    { confPositions  = 0
    , confVelocities = 0.1
    }

pendulumMain :: IO ()
pendulumMain =
    mapM_ (disp 3 . phasePositions)  -- position with 2 digits of precision
  . take 25                          -- 25 steps
  $ runSystem pendulum 0.1 (toPhase pendulum pendulumConfig0)

This pendulum should wobble back and forth, ever so slightly, around equilibrium.

ghci> :l Hamilton.hs
ghci> pendulumMain
0
0.010
0.020
0.029
0.037
0.042
0.045
0.044
0.040
0.032
0.021
0.007
-0.008
-0.023
-0.038
-0.051
-0.061
-0.068
-0.069
-0.065
-0.056
-0.041
-0.022
-0.000
0.023

We see our \(\theta\) coordinate increasing, then turning around and decreasing, swinging the other way past equilibrium, and then turning around and heading back!⁷

We automatically generated equations of motion for a pendulum. Sweet!

Wrap-Up

We traveled through the world of physics, math, Haskell, and back again to achieve something that would have initially seemed like a crazy thought experiment. But, utilizing Hamiltonian mechanics, we have a system that can automatically generate equations of motion given your coordinate system and a potential energy function. We also learned how to leverage typed vectors for more correct code and a smoother development process.

See my previous post for even crazier examples – involving multiple objects, double pendulums, and more. And check out my hamilton library on hackage, which includes demos for exotic interesting systems, rendered graphically on your terminal.

I realize that this was a lot, so if you have any questions or suggestions for clarifications, feel free to leave a comment, drop me a tweet, or find me on the freenode #haskell channel (where I usually idle as jle`!)