Lenses embody Products, Prisms embody Sums

I’ve written about a variety of topics on this blog, but one thing I haven’t touched in too much detail is the topic of lenses and optics. A big part of this is because there are already so many great resources on lenses.

This post won’t be a “lens tutorial”, but rather a dive into an perspective on lenses and prisms that I’ve heard repeated many times (usually credited to Edward Kmett, but shachaf has helped me trace the origins back to this paste by Reid Barton) but never quite expanded on in-depth. In particular, I’m going to talk about the perspective of lenses and prisms as embodying the essences of products and sums (respectively), the insights that perspective brings, how well it flows into the “profunctor optics” formulation, and how you can apply these observations to practical usage of lenses and prisms.

The “final code” in this post is available online as a “stack executable” that, when run, will pop you into a ghci session with all of the final definitions in scope, so you can play around with them :)

An Algebraic Recap

In Haskell, “products and sums” can roughly be said to correspond to “tuples and Either”. If I have two types A and B, (A, B) is their “product” type. It’s often called an “anonymous product”, because we can make one without having to give it a fancy name. It’s called a product type because if A has \(n\) possible values and B has \(m\) possible values, then (A, B) has \(n \times m\) possible values¹. And, Either A B is their (anonymous) “sum” type. It’s called a sum type because Either A B has \(n + m\) possible values. I won’t go much deeper into this, but there are many useful summaries already online on this topic!

Let’s Get Productive!

It’s easy to recognize (Int, Bool) as a product between Int and Bool. However, did you know that some types are secretly product types in disguise?

For example, here’s a classic example of a data type often used with lens:

-- source: https://github.com/mstksg/inCode/tree/master/code-samples/misc/lenses-and-prisms.hs#L145-L148

data Person = P
    { _pName :: String
    , _pAge  :: Int
    }

Person is an algebraic data type — so-called because it is actually a product between a String and Int. Person is isomorphic to (String, Int). I will be writing this as Person <~> (String, Int).

By isomorphic, I mean that there are functions split :: Person -> (String, Int) and unsplit :: (String, Int) -> Person where unsplit . split = id and split . unsplit = id. You can think of this property as stating formally that you should be able to go from one type to the other without “losing any information”. Every single item in one type gets paired to a specific item in the other, and vice versa, and neither type is “too big” or “too small”.

In our case, we have:

split :: Person -> (String, Int)
split (P n a) = (n, a)

unsplit :: (String, Int) -> Person
unsplit (n, a) = P n a

And we can verify that unsplit . split is id:

unsplit . split :: Person -> Person
unsplit . split
    = \x          -> unsplit (split x)        -- substitute definition of (.)
    = \case P n a -> unsplit (split (P n a))  -- expand patterns
    = \case P n a -> unsplit (n, a)           -- substitute definition of split
    = \case P n a -> P n a                    -- substitute definition of unsplit
    = \x      -> x                            -- condense patterns
    = id                                      -- definition of id

And verification of split . unsplit = id is left as an exercise.

There are some other interesting products in Haskell, too. One such example is NonEmpty a (the type of a non-empty list) being a product between a (the head/first item) and [a] (the tail/rest of the items). This means that NonEmpty a is isomorphic to (a, [a]) — we have NonEmpty a <~> (a, [a])! This is witnessed by functions split :: NonEmpty a -> (a, [a]) and unsplit :: (a, [a]) -> NonEmpty a where unsplit . split = id and split . unsplit = id. See if you can write these!

Another curious product is the fact that every type a is a product between itself and unit, (). Every type a is isomorphic to (a, ()) (which follows from the algebraic property \(x * 1 = x\)). Freaky, right?

-- a <~> (a, ())

split :: a -> (a, ())
split x = (x, ())

unsplit :: (a, ()) -> a
unsplit (x, _) = x

One final interesting “product in disguise” is Either a a. “But wait,” you say. “That’s a sum…right??”

Well, yeah. But in addition, any Either a a is the product between Bool and a. We can say that Either a a is isomorphic to (Bool, a)! The Bool tells you “left or right?” and the a is the contents:

-- Either a a <~> (Bool, a)

split :: Either a a -> (Bool, a)
split (Left  x) = (False, x)
split (Right x) = (True , x)

unsplit :: (Bool, a) -> Either a a
unsplit (False, x) = Left  x
unsplit (True , x) = Right x

Proving that unsplit . split = id:

unsplit . split :: Either a a -> Either a a
unsplit . split =
    = \x            -> unsplit (split x)          -- substitute definition of (.)
      -- trying case 1
    = \case Left  y -> unsplit (split (Left  y))  -- expand pattern for case 1
    = \case Left  y -> unsplit (False, y)         -- substitute definition of split
    = \case Left  y -> Left  y                    -- substitute definition of unsplit
    = \x            -> x                          -- condense pattern for case 1
    = id                                          -- definition of id
      -- trying case 2
    = \case Right y -> unsplit (split (Right y))  -- expand pattern for case 2
    = \case Right y -> unsplit (True , y)         -- substitute definition of split
    = \case Right y -> Right y                    -- substitute definition of unsplit
    = \x            -> x                          -- condense pattern for case 2
    = id                                          -- definition of id

And split . unsplit = id is again left as an exercise.

(\case here is from the -XLambdaCase extension)

Lenses

So, how do lenses come into the picture?

Let’s review a bit. A Lens' s a is a way to “access” an a “inside” an s, respecting some laws.

A Lens' s a is a data type with the following API:

view :: Lens' s a -> (s -> a)                -- get the 'a' from an 's'
set  :: Lens' s a -> (a -> s -> s)           -- set the 'a' inside an 's'

respecting the lens laws — get-put, put-get, and put-put. Abstract mathematical laws are great and all, but I’m going to tell you a secret that subsumes those laws.

At first, you might naively implement lenses like:

data Lens' s a = Lens'
    { view :: s -> a
    , set  :: a -> s -> s
    }

But this is bad bad bad. That’s because you can use this to represent lenses that “break the laws”. This representation is, to use the technical term, “too big”. It allows more more values than are actual lenses. It breaks the “make illegal things unrepresentable” principle by a pretty big margin.

So, here’s the secret: A Lens' s a is nothing more than a way of saying that s is a product between a and some type q.

That means that if it is possible to represent s as some (v, w) (or, s <~> (v, w)), then you have two lenses! Lenses are nothing more than descriptions of products! Another way to think of this is that if you are able to “split” a type into two parts without losing any information, then each part represents a lens.

A Lens' s a is nothing more than a witness for the fact that there exists some q where s <~> (a, q).

With that in mind, let’s re-visit a saner definition of lenses based on the idea that lenses embody descriptions of products:

-- | s <~> (a, q)
-- source: https://github.com/mstksg/inCode/tree/master/code-samples/misc/lenses-and-prisms.hs#L81-L84

data Lens' s a = forall q. Lens'
    { split   :: s -> (a, q)
    , unsplit :: (a, q) -> s
    }

Now, if split and unsplit form an isomorphism, this can only represent valid lenses!²

(The forall q. is the -XExistentialQuantification extension, and allows us to hide type variables in constructors. Note that this disallows us from using split and unsplit as record accessors functions, so we have to pattern match to get the contents)

We can implement our necessary lens API as so:

-- source: https://github.com/mstksg/inCode/tree/master/code-samples/misc/lenses-and-prisms.hs#L122-L127

view :: Lens' s a -> (s -> a)
view Lens'{..} = fst . split

set :: Lens' s a -> (a -> s -> s)
set Lens'{..} newVal x = case split x of
    (_, q) -> unsplit (newVal, q)      -- "replace" the `a`

(Using the -XRecordWildcards extension, where Lens'{..} binds split and unsplit to the fields of the lens)

The implementation of the helper function over (which modifies the a with a function) is also particularly elegant:

-- source: https://github.com/mstksg/inCode/tree/master/code-samples/misc/lenses-and-prisms.hs#L129-L130

overL :: Lens' s a -> (a -> a) -> (s -> s)
overL Lens'{..}  f = unsplit . first f . split   -- instance Bifunctor (,)

The surprising result of this perspective is that every product yields lenses (one for every item in the product), and every lens witnesses one side of a product.

Insights Gleaned

Let’s take a look at our first product we talked about:

-- source: https://github.com/mstksg/inCode/tree/master/code-samples/misc/lenses-and-prisms.hs#L145-L148

data Person = P
    { _pName :: String
    , _pAge  :: Int
    }

Because Person is a product between String and Int, we get two lenses: a Lens' Person String and Lens' Person Int. Every product gives us a lens for every item in the product.

-- Person <~> (String, Int)
-- source: https://github.com/mstksg/inCode/tree/master/code-samples/misc/lenses-and-prisms.hs#L150-L160

pName :: Lens' Person String
pName = Lens'
    { split   = \(P n a) -> (n, a)
    , unsplit = \(n, a)  -> P n a
    }

pAge :: Lens' Person Int
pAge = Lens'
    { split   = \(P n a) -> (a, n)
    , unsplit = \(a, n)  -> P n a
    }

These are actually the typical lenses associated with records! You get exactly these lenses if you use makeLenses from the lens package.

The inverse is true too. Every lens witnesses a product. The fact that we have a lawful pName :: Lens' Person String means that a Person must be a product between String and some other (hidden) type.

It can be insightful to look at products that we know and see what lenses those correspond to.

For example, our NonEmpty a <~> (a, [a]) product tells us that NonEmpty a has at least two lenses: a “head” lens Lens' (NonEmpty a) a and a “tail” lens Lens' (NonEmpty a) [a].

Our a <~> (a, ()) product gives some interesting insight. This tells us that we always have an “identity” lens Lens' a a, and a “unit” lens Lens' a (), for any a:

-- a <~> (a, ())
-- source: https://github.com/mstksg/inCode/tree/master/code-samples/misc/lenses-and-prisms.hs#L162-L172

identityL :: Lens' a a
identityL = Lens'
    { split   = \x      -> (x, ())
    , unsplit = \(x, _) -> x
    }

united :: Lens' a ()
united = Lens'
    { split   = \x       -> ((), x)
    , unsplit = \((), x) -> x
    }

In the language of lens, identityL :: Lens' a a tells us that all as have an a “inside” them. However, in the language of products, this just tells us that a can be represented as (a, ()). In the language of lens, united :: Lens' a () tells us that all as have a () “inside” them. In the language of products, this just tells us that a <~> (a, ()).

What insight does our Either a a <~> (Bool, a) product perspective give us? Well, let’s write out their types and see what it might suggest:

-- source: https://github.com/mstksg/inCode/tree/master/code-samples/misc/lenses-and-prisms.hs#L174-L184

mysteryLens1 :: Lens' (Either a a) Bool

mysteryLens2 :: Lens' (Either a a) a

Looking at mysteryLens1 :: Lens' (Either a a) Bool, we are saying that every Either a a has some Bool “inside” it. From our knowledge of our product, we know that this Bool is really a flag for left-ness or right-ness. Getting the Bool is finding out if we’re in Left or Right, and flipping the Bool “inside” is really just swapping from Left to Right.

-- source: https://github.com/mstksg/inCode/tree/master/code-samples/misc/lenses-and-prisms.hs#L194-L198

flipEither :: Either a a -> Either a a
flipEither = overL mysteryLens1 not

isRight :: Either a a -> Bool
isRight = view mysteryLens1

ghci> flipEither (Left 'a')
Right 'a'
ghci> flipEither (Right 'a')
Left 'a'
ghci> isRight (Left 'a')
False
ghci> isRight (Right 'a')
True

If we think about lenses as embodying “record fields” (things that give you the ability to “get” a field, and “modify” a field — corresponding with view and set), we can think of mysteryLens1 as an abstract record field into the Leftness/Rightness of a value. Thinking of lenses as defining abstract record fields is a common tool for backwards compatibility.

Looking at mysteryLens2 :: Lens' (Either a a) a, we are saying that every Either a a has some a “inside” it. From what we know about the underlying product, the a is just the “contained value”, ignoring leftness or rightness. Getting the a is getting the contained value and losing leftness/rightness, and re-setting the a inside is modifying the contained value but preserving leftness/rightness.

-- source: https://github.com/mstksg/inCode/tree/master/code-samples/misc/lenses-and-prisms.hs#L200-L204

fromEither :: Either a a -> a
fromEither = view mysteryLens2

mapEither :: (a -> a) -> Either a a -> Either a a
mapEither = overL mysteryLens2

ghci> fromEither (Left 'a')
'a'
ghci> mapEither negate (Left 3)
Left (-3)
ghci> mapEither negate (Right 4)
Right (-4)

So that’s really the essence of what a Lens' is. A Lens' s a is the embodiment of the fact that s can be represented as a product between a and something else — that s <~> (a, q). All of the lens laws just boil down to this. Lenses embody products.

"Sum-thing" Interesting

It’s easy to recognize Either Int Bool as a sum between Int and Bool. However, did you know that some types are secretly sums in disguise?

For example, here’s a data type you might encounter out there in the real world:

-- source: https://github.com/mstksg/inCode/tree/master/code-samples/misc/lenses-and-prisms.hs#L221-L222

data Shape = Circle  Double           -- radius
           | RegPoly Natural Double   -- number of sides, length of sides

Circle 2.9 represents a circle with radius 2.9, and RegPoly 8 4.6 represents a octagon (8-sided figure) whose sides all have length 4.6.

Shape is an algebraic data type — so-called because it is actually a sum between Double and (Natural, Double) (a Natural is the non-negative Integer type). Shape is isomorphic to Either Double (Natural, Double). To prove it, let’s witness Shape <~> Either Double (Natural, Double) using the functions match and inject:

-- Shape <~> Either Double (Natural, Double)

match :: Shape -> Either Double (Natural, Double)
match (Circle  r  ) = Left r
match (RegPoly n s) = Right (n, s)

inject :: Either Double (Natural, Double) -> Shape
inject (Left   r    ) = Circle  r
inject (Right (n, s)) = RegPoly n s

Since inject . match = id and match . inject = id, this proves that Shape is a sum in disguise.

Another interesting “hidden sum” is the fact that [a] in Haskell is actually a sum between () and (a, [a]). That’s right — it’s a sum between () and…itself with a value? Indeed it is pretty bizarre.

However, if we think of () as the possibility of an empty list, and (a, [a]) as the possibility of NonEmpty a (the “head” of a list consed with the rest of the list), then saying that [a] is a sum between () and NonEmpty a is saying that [a] is “either an empty list or a non-empty list”. Whoa. Take that, LEM denialists.³

-- [a] <~> Either () (NonEmpty a)

match :: [a] -> Either () (NonEmpty a)
match []     = Left  ()
match (x:xs) = Right (x :| xs)

inject :: Either () (NonEmpty a) -> [a]
inject (Left   _       ) = []
inject (Right (x :| xs)) = x:xs

-- [a] <~> Either () ([a], a)

match  :: [a] -> Either () ([a], a)
match xs
  | null xs   = Left  ()
  | otherwise = Right (init xs, last xs)

-- init gives you all but the last item:
-- > init [1,2,3] = [1,2]

inject :: Either () (a, [a]) -> [a]
inject (Left   _     ) = []
inject (Right (xs, x)) = xs ++ [x]

Another curious sum: if we consider the “empty data type” Void, the type with no inhabitants:

-- source: https://github.com/mstksg/inCode/tree/master/code-samples/misc/lenses-and-prisms.hs#L224-L229

data Void           -- no constructors, no valid inhabitants

absurd :: Void -> a     -- A useful helper function when working with `Void`
absurd = \case -- empty case statement because we have
               -- no constructors of 'Void' we need to
               -- match on

then we have an interesting sum: every type a is a sum between itself and Void. In other words, a is isomorphic to Either a Void (which follows from the algebraic property \(x + 0 = x\)):

-- a <~> Either a Void

match :: a -> Either a Void
match x = Left x

inject :: Either a Void -> a
inject (Left  x) = x
inject (Right v) = absurd v

Again, if you don’t believe me, verify that inject . match = id and match . inject = id!⁴

One final example: earlier, we said that every type can be decomposed as a product involving (). Algebraically, finding that mystery type is easy — we solve \(x = 1 * y\) for \(y\) (since () is 1), and we see \(y = x\). This tells us that every type is a product between () and itself (a <~> ((), a)).

However, can every type be decomposed as a sum involving ()?

Algebraically, we need to find this mystery type by solving \(x = 1 + y\) for \(y\), and the result is \(y = x - 1\). We can interpret \(x - 1\) as “a, minus one potential element”.

This type isn’t expressible in general in Haskell, so no, not every type can be decomposed as a sum involving (). The necessary and sufficient condition is that there must exist some type that is the same as your original type but with one missing element.

Oh, hey! Remember our [a] <~> Either () (NonEmpty a) decomposition? That’s exactly this! Here, NonEmpty a is our mystery type: it’s exactly a list [a] minus one potential element (the empty list).

There’s another way to go about this: we can talk about \(x - 1\) by specifying one single “forbidden element”. This isn’t explicitly possible in Haskell, but we can simulate this by using an abstract type. We have this ability using “refinement types”. For example, using the refined library, a Refined (NotEqualTo 4) Int is a type that is the same as Int, except the 4 value is forbidden.

We can use it to implement a Int <~> Either () (Refined (NotEqualTo 4) Int) witness:

-- | Like `Int`, but cannot be constructed if it is 4
type Not4 = Refined (NotEqualTo 4) Int

-- | Provided by the 'refined' library that lets us refine and unrefine a type
refineFail :: Int  -> Maybe Not4
unrefine   :: Not4 -> Int


-- | The "safe constructor"
match :: Int -> Either () Not4
match n = case refineFail n of
    Nothing -> Left ()          -- the value was 4, so we return `Left`
    Just x  -> Right x          -- value was successfully refined

-- | The "safe extractor"
inject :: Either () Not4 -> Int
inject (Left  _) = 4
inject (Right x) = unrefine x

In fact, if we can parameterize an isomorphism on a specific value, all types with at least one value can be expressed as a sum involving ()! It’s always () plus the type itself minus that given specific value. (In practice, this is only possible to represent in Haskell if we can test for equality)

Through the Looking-Prism

Now let’s bring prisms into the picture. A Prism' s a also refers to some a “possibly inside” an s, with the following API: preview and review⁵

preview :: Prism' s a -> (s -> Maybe a)   -- get the 'a' in the 's' if it exists
review  :: Prism' s a -> (a -> s)         -- reconstruct the 's' from an 'a'

If you think of a prism as representing an abstract constructor, the preview is the “pattern match”, and the review is the “constructing”.

Naively you might implement a prism like this:

data Prism' s a = Prism'
    { preview :: s -> Maybe a
    , review  :: a -> s
    }

But, again, this implementation space is too big. There are way too many values of this type that aren’t actual “lawful” prisms. And the laws are kind of muddled here.

You might be able to guess where I’m going at this point. Whereas a Lens' s a is nothing more than a witness to the fact that s is a product (a, q) … a Prism' s a is nothing more than a witness to the fact that s is a sum Either a q. If it is possible to represent s as some Either v w…then you have two prisms! Prisms are nothing more than descriptions of sums! If you are able to “split” a type into one of two possibilities, then each possibility represents a prism.

A Prism' s a is nothing more than saying that there exists some type q that can be used to witness a s <~> Either a q isomorphism.

Under this interpretation, we can write a nice representation of Prism':

-- | s <~> Either a q
-- source: https://github.com/mstksg/inCode/tree/master/code-samples/misc/lenses-and-prisms.hs#L100-L103

data Prism' s a = forall q. Prism'
    { match  :: s -> Either a q
    , inject :: Either a q -> s
    }

If match and inject form an isomorphism, this can only represent valid prisms!

We can now implement the prism API:

-- source: https://github.com/mstksg/inCode/tree/master/code-samples/misc/lenses-and-prisms.hs#L132-L138

preview :: Prism' s a -> (s -> Maybe a)
preview Prism'{..} x = case match x of
    Left  y -> Just y
    Right _ -> Nothing

review  :: Prism' s a -> (a -> s)
review Prism'{..} = inject . Left

Like for lenses, prisms also admit a particularly elegant formulation for over, which maps a function over the a in the s if it exists:

-- source: https://github.com/mstksg/inCode/tree/master/code-samples/misc/lenses-and-prisms.hs#L129-L141

overL :: Lens' s a -> (a -> a) -> (s -> s)
overL Lens'{..}  f = unsplit . first f . split   -- instance Bifunctor (,)

overP :: Prism' s a -> (a -> a) -> (s -> s)
overP Prism'{..} f = inject . first f . match    -- instance Bifunctor Either

Neat, they’re actually exactly identical! Who would have thought?

So we see now, similar to lenses, every sum yields prisms, and every prism witnesses one side of a sum.

Prism Wisd’m

Let’s go back at our example prisms and see what sort of insight we can gain from this perspective.

-- source: https://github.com/mstksg/inCode/tree/master/code-samples/misc/lenses-and-prisms.hs#L221-L222

data Shape = Circle  Double           -- radius
           | RegPoly Natural Double   -- number of sides, length of sides

Because Shape is a sum between Double and (Natural, Double), we get two prisms:

-- Shape <~> Either Natural (Natural, Double)
-- source: https://github.com/mstksg/inCode/tree/master/code-samples/misc/lenses-and-prisms.hs#L231-L249

_Circle :: Prism' Shape Double
_Circle = Prism'
    { match  = \case
        Circle  r    -> Left r
        RegPoly n s  -> Right (n, s)
    , inject = \case
        Left   r     -> Circle r
        Right (n, s) -> RegPoly n s
    }

_RegPoly :: Prism' Shape (Natural, Double)
_RegPoly = Prism'
    { match  = \case
        Circle  r    -> Right r
        RegPoly n s  -> Left (n, s)
    , inject = \case
        Left  (n, s) -> RegPoly n s
        Right  r     -> Circle r
    }

And these are actually the typical prisms associated with an ADT. You actually get exactly these if you use makePrisms from the lens package.

If it isn’t clear what’s going on, let’s look at the type of preview and review for _Circle:

preview _Circle :: Shape   -> Maybe Natural
review  _Circle :: Natural -> Shape

We essentially get the ability to “pattern match” and “construct” the Circle constructor.

What can we get out of our decomposition of [a] as a sum between () and NonEmpty a? Let’s look at them:

-- [a] <~> Either () (NonEmpty a)
-- source: https://github.com/mstksg/inCode/tree/master/code-samples/misc/lenses-and-prisms.hs#L251-L269

_Nil :: Prism' [a] ()
_Nil = Prism'
    { match  = \case
        []              -> Left ()
        x:xs            -> Right (x :| xs)
    , inject = \case
        Left _          -> []
        Right (x :| xs) -> x:xs
    }

_Cons :: Prism' [a] (NonEmpty a)
_Cons = Prism'
    { match  = \case
        []              -> Right ()
        x:xs            -> Left (x :| xs)
    , inject = \case
        Left  (x :| xs) -> x:xs
        Right _         -> []
    }

To clarify, we can look at preview and review for all of these:

preview _Nil  :: [a] -> Maybe ()
preview _Cons :: [a] -> Maybe (NonEmpty a)

review  _Nil  :: ()         -> [a]
review  _Cons :: NonEmpty a -> [a]

It looks like the () branch’s preview corresponds to a prism that matches on an empty list, and the NonEmpty a branch corresponds to a prism that matches on a non-empty list. And the () branch’s review corresponds to constructing an empty list, and the NonEmpty a branch corresponds to constructing a non-empty list.

-- source: https://github.com/mstksg/inCode/tree/master/code-samples/misc/lenses-and-prisms.hs#L271-L289

_Nil' :: Prism' [a] ()
_Nil' = Prism'
    { match  = \xs -> if null xs
        then Left  ()
        else Right (init xs, last xs)
    , inject = \case
        Left _        -> []
        Right (xs, x) -> xs ++ [x]
    }

_Snoc :: Prism' [a] ([a], a)
_Snoc = Prism'
    { match  = \xs -> if null xs
        then Right ()
        else Left  (init xs, last xs)
    , inject = \case
        Left  (xs, x) -> xs ++ [x]
        Right _       -> []
    }

And, looking at a <~> Either a Void…what does that decomposition give us, conceptually?

-- a <~> Either a Void
-- source: https://github.com/mstksg/inCode/tree/master/code-samples/misc/lenses-and-prisms.hs#L291-L306

identityP :: Prism' a a
identityP = Prism'
    { match = Left
    , inject = \case
        Left  x -> x
        Right v -> absurd v
    }

_Void :: Prism' a Void
_Void = Prism'
    { match = Right
    , inject = \case
        Left  v -> absurd v
        Right x -> x
    }

In lens-speak, identityP :: Prism' a a tells us that all as have an a “inside” them (since match always matches) and that you can construct an a with only an a (whoa). In our “sum” perspective, however, it just witnesses that an a <~> Either a Void sum.

In lens-speak, _Void :: Prism' a Void tells us that you can pattern match a Void out of any a (and that match will always fail). Furthermore, it tells us that if you have a value of type Void, you can use the _Void “constructor” to make a value of any type a! We have review _Void :: Void -> a!

However, in our “sum” perspective, it is nothing more than the witness of the fact that a is the sum of a and Void.

And finally, let’s look at our deconstruction of Int and Refined (NotEqualTo 4) Int. What prisms does this yield, and what insight do we get?

-- source: https://github.com/mstksg/inCode/tree/master/code-samples/misc/lenses-and-prisms.hs#L308-L328

type Not4 = Refined (NotEqualTo 4) Int

only4 :: Prism' Int ()
only4 = Prism'
    { match  = \n -> case refineFail n of
        Nothing -> Left ()
        Just x  -> Right (x :: Not4)
    , inject = \case
        Left  _ -> 4
        Right x -> unrefine x
    }

refined4 :: Prism' Int Not4
refined4 = Prism'
    { match  = \n -> case refineFail n of
        Nothing -> Right ()
        Just x  -> Left x
    , inject = \case
        Left  x -> unrefine x
        Right _ -> 4
    }

The first prism, only4, is a prism that basically “only matches” on the Int if it is 4. We can use it to implement “is equal to four”, and “get a 4”

-- source: https://github.com/mstksg/inCode/tree/master/code-samples/misc/lenses-and-prisms.hs#L330-L334

isEqualTo4 :: Int -> Bool   -- Checks if a value is 4
isEqualTo4 = isJust . preview only4

four :: Int     -- Is simply `4`
four = review only4 ()

The name only4 is inspired by the only combinator from the lens library, which lets you provide a value you want to “restrict”.

-- | From the lens library; lets you provide the value you want to "restrict"
only :: Eq a => a -> Prism' a ()

only4 :: Prism' Int ()
only4 = only 4

The second prism, refined4, basically acts like a “abstract (smart) constructor” for Not4, essentially refineFail and unrefine:

-- source: https://github.com/mstksg/inCode/tree/master/code-samples/misc/lenses-and-prisms.hs#L336-L340

makeNot4 :: Int -> Maybe Not4
makeNot4 = preview refined4

fromNot4 :: Not4 -> Int
fromNot4 = review refined4

Prism or Not

To me, one of the most useful things about this prism perspective is that it helps me see what isn’t a prism.

For example, is it possible to have a prism into the head of a list? That is, is the following prism possible?

_head :: Prism' [a] a           -- get the head of a list

If you think of a prism as just “a lens that might fail” (as it’s often taught), you might think yes. If you think of a prism as just “a constructor and deconstructor”, you might also think yes, since you can construct an [a] with only a single a.⁶ You can definitely “implement” this prism incorrectly naively, in terms of preview and review, and it would still typecheck.

Both of these viewpoints of prisms will fail you and lead you astray.

However, if you think of it as witnessing a sum, you might see that this prism isn’t possible. There is no possible type q where [a] is a sum of a and q, where the a matches the head of the list. No q works. There is no way to express [a] as the sum of a and some other type (where the a represents the head of a list). Try thinking of a type q — it’s just not possible!⁷

match :: [a] -> Either a MysteryType
match []     = Right mysteryValue
match (x:xs) = Left x                       -- will we lose `xs`?

inject :: Either a MysteryType -> [a]
inject (Left x)  = x:????                   -- yes, we lost `xs`
inject (Right v) = []

From this attempt, we see that no matter what q we pick, we will “lose xs”. There’s no way to “store” the tail of the list in match in order to recover it later in inject.

The Path to Profunctors

As a finale, I’d like to show how these dual perspectives (lenses are witnesses to products and prisms are witnesses to sum) make their implementation in terms of “profunctor optics” very natural.

First, some background – a “profunctor optic” is a way of expressing things like lenses and prisms in terms of “profunctor value transformers”. Lenses, prisms, etc. would not be record types, but rather functions that takes a profunctor value and return a new profunctor value.

A profunctor p has values of type p a b, and you can roughly think of p a b (a profunctor value) as “a relationship between a and b”.

The Profunctor typeclass p gives us a few functions. We can use them to create a function that transforms a profunctor value in terms of an isomorphism.

If type s is isomorphic to type a (s <~> a), then we can the function iso, that the Profunctor class gives us:

iso :: Profunctor p
    => (s -> a)         -- ^ one half of the isomorphism
    -> (a -> s)         -- ^ the other half of the isomorphism
    -> p a a
    -> p s s
iso = dimap         -- `dimap` comes from the `Profunctor` typeclass

Given the s -> a and a -> s functions that witness s <~> a, we can use iso (defined using Profunctor typeclass methods) to transform a p a a into a p s s (a relationship on as to be a relationship on s) according to an isomorphism.

Profunctor Lens

A “profunctor lens” (which is a specific way of implementing lenses) Lens' s a is a function:

p a a -> p s s

You can think of it as taking a “relationship on as” and turning it into a “relationship on ss”.

With a lens, we are saying that s is isomorphic to (a, q). That means that we have, at our disposal:

iso split unsplit
    :: Profunctor p
    => p (a, q) (a, q)
    -> p s s

With that, in order to get a p a a -> p s s, we need a way to turn a p a a into a p (a, q) (a, q). This says “take a relationship on as and turn it into a relationship on (a, q), ignoring the q”.

There happens to be a typeclass called Strong that gives us just that!

-- | The "operate on a part of a whole" typeclass
class Profunctor p => Strong p where
    first'
        :: p a b                -- ^ relationship on part
        -> p (a, q) (b, q)      -- ^ relationship on whole

And so we now have a definition of a profunctor lens:

-- source: https://github.com/mstksg/inCode/tree/master/code-samples/misc/lenses-and-prisms.hs#L361-L369

makeLens
    :: Strong p
    => (s -> (a, q))        -- ^ split
    -> ((a, q) -> s)        -- ^ unsplit
    -> p a a                -- ^ relationship on a
    -> p s s                -- ^ relationship on s
makeLens split unsplit =
    iso split unsplit  -- ^ p (a, q) (a, q) -> p s s
  . first'             -- ^ p a a -> p (a, q) (a, q)

makeLens split unsplit :: Strong p => p a a -> p s s is a profunctor lens (a “profunctor value transformer”)!

Essentially, iso split unsplit . first' promotes a p a a to a p s s. It uses first' to turn the p a a into a p (a, q) (a, q), turning a relationship on the part to be a relationship on the whole. Then we just apply the essential s <~> (a, q) isomorphism that defines a lens. And so p a a -> p s s, going through the s <~> (a, q) isomorphism, is a lens!

Profunctor Prisms

A profunctor prism (one way of implementing) Prism' s a is a function:

p a a -> p s s

You can also think of this as taking a “relationship on as” and turning it into a “relationship on ss”.

With a prism, we are saying that s is isomorphic to Either a q. That means that we have, at our disposal:

iso match inject
    :: Profunctor p
    => p (Either a q) (Either a q)
    -> p s s

With that tool in hand, in order to get a p a a -> p s s, we need a way to turn a p a a into a p (Either a q) (Either a q). This says “take a relationship on as and turn it into a relationship on Either a q, doing nothing if the q pops up”.

Luckily, there happens to be a typeclass called Choice that gives us exactly that!

-- | The "operate on a branch of a possibility" typeclass
class Profunctor p => Choice p where
    left'
        :: p a b                        -- ^ relationship on branch
        -> p (Either a q) (Either b q)  -- ^ relationship on all possibilities

And so we now have a definition of a profunctor prism:

-- source: https://github.com/mstksg/inCode/tree/master/code-samples/misc/lenses-and-prisms.hs#L371-L379

makePrism
    :: Choice p
    => (s -> Either a q)    -- ^ match
    -> (Either a q -> s)    -- ^ inject
    -> p a a                -- ^ relationship on a
    -> p s s                -- ^ relationship on s
makePrism match inject =
    iso match inject   -- ^ p (Either a q) (Either a q) -> p s s
  . left'              -- ^ p a a -> p (Either a q) (Either a q)

makeLens match inject :: Choice p => p a a -> p s s is a profunctor prism (a “profunctor value transformer”)!

Essentially, iso match inject . left' promotes a p a a to a p s s. It uses left' to turn the p a a into a p (Either a q) (Either a q), turning a relationship on the part to be a relationship on the whole. Then we just apply the essential s <~> Either a q isomorphism that defines a prism. And so p a a -> p s s, going through the s <~> Either a q isomorphism, is a prism!

-- | `(View a) s s` is just an `s -> a`
newtype View a s r = View { runView :: s -> a }

instance Profunctor (View a)
instance Strong (View a)

Motivation

To me, this perspective makes it really clear to see “why” profunctor lenses and profunctor prisms are implemented the way they are. At first, the profunctor optics definitions seemed really opaque and arbitrary to me, and I had no idea why Strong and Choice corresponded to lenses and prisms.

But now, I know that lenses are prisms can be seen as just profunctor value transformers that transform along the decomposition that the lenses and prisms represent. For profunctor lenses, the profunctor values get transformed to “parts of a whole” profunctor values, using Strong. For profunctor prisms, the profunctor values get transformed to “branches of a possibility” profunctor values, using Choice. Even their types clearly show what is going on:

-- [Lens]  s <~> (a, q)
first' :: p a a -> p (a, q) (a, q)

-- [Prism] s <~> Either a q
left'  :: p a a -> p (Either a q) (Either a q)

In fact, Strong and Choice fit lenses and prisms like a glove so well that sometimes I wonder if Edward Kmett just invented those typeclasses custom-made to represent lenses and prisms.

Or…maybe lenses and prisms were invented custom-made based on Strong and Choice?

Closing out

Hopefully this perspective — that products yield lenses and sums yield prisms — helps you navigate how you discover lenses and prisms, and how you interpret them when you see them. I know for me, it has helped me understand the odd lenses and prisms I often see, and also it helps me reason about when it doesn’t make sense to have a lens or prism. It has also distilled the lens and prism laws into something trivial that can be stated succinctly (“it must be an isomorphism”), and also made the profunctor optics form seem uncannily natural.

The rest of this post describes small notes that bridge this view to the way lenses and prisms are actually implemented in real life, by clarifying what lens families (and “type-changing lenses”) are in this view, and also how we sometimes get away with using an abstract q type. At the end, there are also exercises and questions (mostly conceptual) to test your understanding!

Lens Families

We have been dealing with Lens' outer inner and Prism' outer inner, which are known as “simple” optics. In practice, this can be generalized by giving the “input” outer/inner values and “output” outer/inner values different type variables.

For example, so far all our operations have basically been navigating between the isomorphisms that lenses and prisms represent:

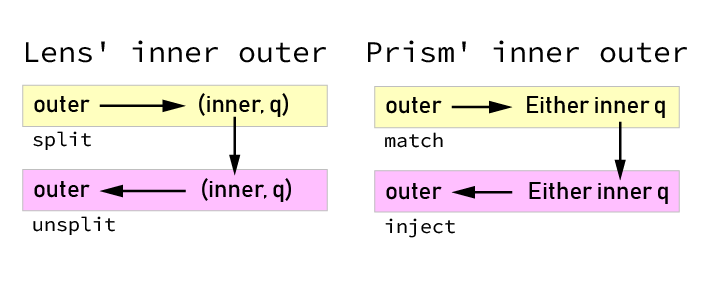
Note how it is kind of complicated to talk about specific parts. If I say “the value of type inner”, do I mean the value “before” we use the lens, or “after” we use the lens? There are two inner-typed values in our picture.

A “Lens family” is a trick we can do to make talking about things easier. We use the same lenses, but we re-label the “before” and “after” (input and output) with different type variables, like so:

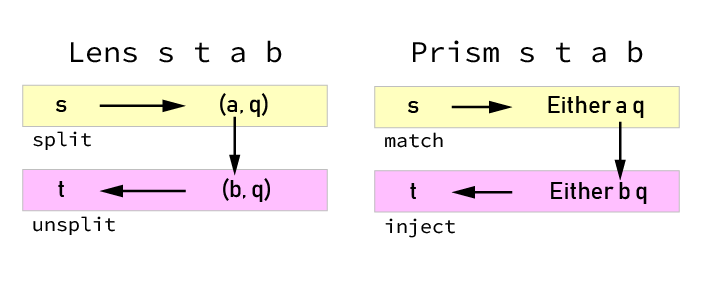
Essentially, we’re just deciding to give the inputs and outputs different type variables. The main thing this helps is with is giving us the ability to distinguish inputs from outputs when we talk about these things.

For example, before, with Lens' outer inner, if I say “the outer”, you won’t know if I mean the outer “before” we use the lens, or the outer after we use the lens. However, with Lens s t a b, if I say “the s”, you know that I just mean “the outer before we use the lens”, and if I say “the t”, you know that I mean “the outer after we use the lens”. The profunctor optics version of lens becomes Lens s t a b = p a b -> p s t.

Lens s t a b (which is a version of Lens' outer inner where we relabel the type variables of the inputs and outputs) is called a lens family. Be careful to never call it a “polymorphic lens”. It is just a normal lens where we re-label the type variables of all of the involved pieces to aid in our discourse. It is often also called a “type-changing lens”.

data Lens s t a b = forall q. Lens
    { split   :: s -> (a, q)        -- before (with s and a)
    , unsplit :: (b, q) -> t        -- after  (with t and b)
    }

view :: Lens s t a b -> (s -> a)
set  :: Lens s t a b -> (b -> s -> t)

data Prism s t a b = forall q. Prism
    { match  :: s -> Either a q     -- before (with s and a)
    , inject :: Either b q -> t     -- after  (with t and b)
    }

matching :: Prism s t a b -> (s -> Either t a)
review   :: Prism s t a b -> (b -> t)

We still require unsplit . split = id, split . unsplit = id, inject . match = id, and match . inject = id. They’re all still isomorphisms. We’re just relabeling our type variables here to let us be more expressive with how we talk about all of the moving parts.

Lens families can also be used to implement “type changing lenses” where tweaking the inner type can cause the outer type to also change appropriately. But s, t, a, and b can’t just be whatever you want. They have to be picked so that unsplit . split and inject . match can typecheck.

Abstract Factors and Addends

In practice, the q to factor out your type into (in the s <~> (a, q) and s <~> Either a q) might not be an actual “concrete” type. In most cases, it’s alright to treat it as a theoretical “abstract” type that follows the behavior you want given a restricted interface. This is “safe” because, if you notice, none of the methods in the lens or prism APIs (view, set, preview, review) ever let an external user directly manipulate a value of type q.

For example, the only 'a' :: Prism' Char () prism matches only on 'a', and it is the sum of Char and a theoretical abstract Char type that excludes 'a'.

To formalize this, sometimes we can say that only “one direction” of the isomorphism has to be strictly true in practice. If we only enforce that the round-trip of unsplit . split = id and inject . match = id, this enforces the “spirit” of the hidden abstract type.

For example, our “only 'a'” can be witnessed by:

-- source: https://github.com/mstksg/inCode/tree/master/code-samples/misc/lenses-and-prisms.hs#L206-L350

type CharButNotA = Char

onlyA :: Prism' Char ()
onlyA = Prism'
    { match  = \case
        'a' -> Left ()
        x   -> Right (x :: CharButNotA)
    , inject = \case
        Left  _ -> 'a'
        Right x -> x        -- Right contains a CharButNotA
    }

This passes inject . match = id, but not match . inject = id if we pass in the “illegal” value Right 'a'.

For an example of a lens where this abstract type perspective is useful, there is the contains 'a' lens for sets:

-- import qualified Data.Set as S

contains 'a' :: Lens' (S.Set Char) Bool

-- check if a set contains an element
view (contains 'a') :: S.Set Char -> Bool

-- force a set to contain or not contain 'a'
set (contains 'a') :: Bool -> S.Set Char -> S.Set Char

-- toggle membership in a set
over (contains 'a') not :: S.Set Char -> S.Set Char

contains 'a' is a lens into a Bool from a S.Set, where the Bool indicates if the set “contains” a or not. What product does this represent?

Well, essentially, Set Char <~> (Bool, Set CharButNotA). It’s an abstract product betweein “the set contains 'a' or not” and a set that could not possibly contain 'a':

-- source: https://github.com/mstksg/inCode/tree/master/code-samples/misc/lenses-and-prisms.hs#L206-L217

type CharButNotA = Char

containsA :: Lens' (S.Set Char) Bool
containsA = Lens'
    { split   = \s ->
        ( 'a' `S.member` s
        , 'a' `S.delete` s      :: S.Set CharButNotA
        )
    , unsplit = \case
        (False, s) -> s
        (True , s) -> 'a' `S.insert` (s :: S.Set CharButNotA)
    }

Again, only unsplit . split = id is technically true. split . unsplit = id will fail if the input set contains 'a'.

Exercises

To help solidify your understanding on this perspective, here are some exercises! Most of them are conceptual and open-ended.

• We discussed the conditions where a type a can be expressed as a sum involving () and you can have a Prism' a ().

  Under what conditions can you express a type a as a product involving Void, and you can have a Lens' a Void? (Hint: use the algebra!) What would this lens do (what are view, set, and over)?

• We discussed the conditions where a type a can be expressed as a product involving () and you can have Lens' a ().

  Under what conditions can you express a type a as a product involving Bool (a <~> (Bool, q)), and you can have a Lens' a Bool? (Hint: use the algebra!) What would this lens do (what are view, set, and over)? And what about the Lens' a q?

• We found that by interpreting Either a a as a product (Bool, a) gives us two interesting lenses:

  leftOrRight :: Lens' (Either a a) Bool
  theContents :: Lens' (Either a a) a

  We concluded that the first lens lets us flip between Left and Right or check if a value was Left or Right, and that the second lens gets into the contents regardless of leftness or rightness.

  However, there’s a flip side, as well. (Bool, a) can be expressed as a sum between a and itself, Either a a. This gives us two prisms:

  -- source: https://github.com/mstksg/inCode/tree/master/code-samples/misc/lenses-and-prisms.hs#L59-L69
  
  mysteryPrism1 :: Prism' (Bool, a) a
  
  mysteryPrism2 :: Prism' (Bool, a) a

  What do these prisms do? What is preview, review, over for them?

• Alright, now time to write code. Another “interesting” product is the fact that Bool -> a is isomorphic to (a, a). That is, Bool -> a is a product between a and itself.

  Can you write the corresponding two Lens' (Bool -> a) as? And, what do they mean? (what are view, set, over for those lenses?) Solutions online

• Can you write combinators to “compose” lenses and prisms? Is it even possible?

  -- source: https://github.com/mstksg/inCode/tree/master/code-samples/misc/lenses-and-prisms.hs#L81-L107
  
  data Lens' s a = forall q. Lens'
      { split   :: s -> (a, q)
      , unsplit :: (a, q) -> s
      }
  
  (.&.) :: Lens' a b
        -> Lens' b c
        -> Lens' a c
  
  data Prism' s a = forall q. Prism'
      { match  :: s -> Either a q
      , inject :: Either a q -> s
      }
  
  (.|.) :: Prism' a b
        -> Prism' b c
        -> Prism' a c

  Roughtly speaking, composition of lenses or prisms are meant to “successively zoom in” to deeper and deeper parts of an initial structure.

  A note for you if you try this — because the q type is existential, you can’t use split, unsplit, match, or inject as record accessors, and you need to either pattern match or use -XRecordWildcards.

  These implementations are pretty hairy (solutions online here), and it’s a sort of testament as to why we don’t use this actual implementation in practice. In fact, for profunctor optics, we just have:

  (.&.) = (.)
  (.|.) = (.)

  Using (.) from Prelude. Definitely much simpler! (And it’s one main reason why they’re among the most popular representation)

Special Thanks

I am very humbled to be supported by an amazing community, who make it possible for me to devote time to researching and writing these posts. Very special thanks to my supporter at the “Amazing” level on patreon, Sam Stites! :)