Breaking a Degenerate Hyper-Dimensional Game of Life
by Justin Le ♦
tldr: Demonstrated with interactive visualizations and simulations — over the course of a month, we were able to discover successive new mathematical properties of a “degenerate” hyper-dimensional game of life” to take a “7 dimensions may just barely be possible on a commercial PC, could we ever reach 10 dimensions?” to “10 dimensions is easy enough to be run on any modern browser (jump to spoilers here), and 60 dimensions can be reached with a compiled language”.
This is a story about breaking a degenerate hyper-dimensional game of life via interactive exploratory visualizations and math!
T’was the night before Thursday, December 17, 2020, the release of “Conway Cubes”. It was Day 17 of Advent of Code 2020, a series of fun little themed coding puzzles building up to Christmas; I always enjoyed these puzzles because they are so self-contained and tidy that they are often open-ended in the interesting ways you can solve them or expand on them (which I’ve written many blog posts on).
On the surface, Day 17 seemed to be a straightforward extension of Conway’s Game Of Life (“GoL”). GoL is a simulation played out on a 2D grid, where cells are “on” and “off”, and at each step of the simulation the states spread and propagate in interesting ways based on the state of their neighbors (a 2D cellular automaton). The twist of the Advent of Code puzzle is it asks what would happen if we played out the rules of GoL in 3D instead, and then 4D.
I submitted my solution on my assigned puzzle input with a naive implementation (placing 66 and 66 on the leaderboards for that day), concluding the “competitive” part. Of course, the real fun always starts after. When discussing with some friends (on the subreddit and freenode’s ##adventofcode channel), we started talking about the trade-offs of different implementations and realized that the extra dimensionality was no joke: as you upped the number of dimensions, the number of points you have to consider grow exponentially, and so does the number of neighbors at each point to check. 4D can be solved naively, but anything higher is going to be strained. My naive solution on 6D took three minutes, and 7D in a reasonable amount of time (requiring as much as 612,220,032 points with 2,186 neighbors each) seemed impossible on commercial consumer hardware because of the sheer number of points in 7D space. But I thought…what if a breakthrough in optimization was possible? I set an (arbitrary) personal goal of reaching 10D (3,570,467,226,624 points with 59,048 neighbors each), not knowing if it would ever be possible.
And soon…a breakthrough did come! Someone brought up that if we look at the 3d version, we see there’s actually a mirror symmetry! Because everything starts off on the xy plane, with z=0, the resulting progression must be symmetrical on both sides (positive and negative z).
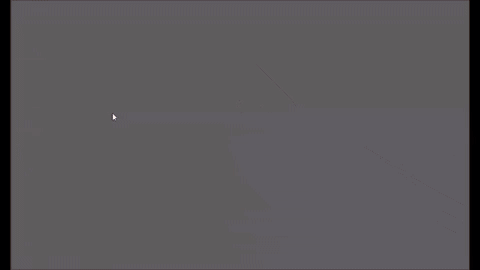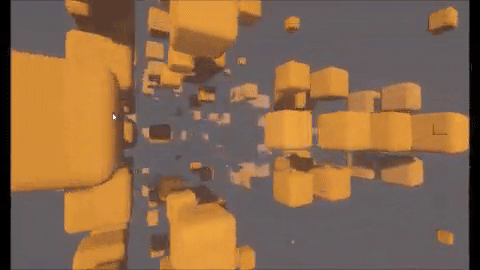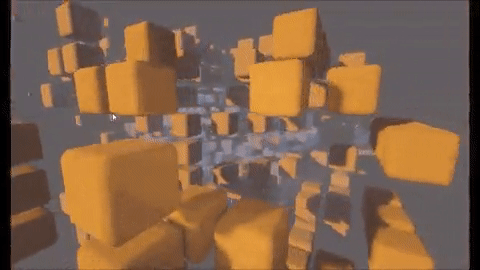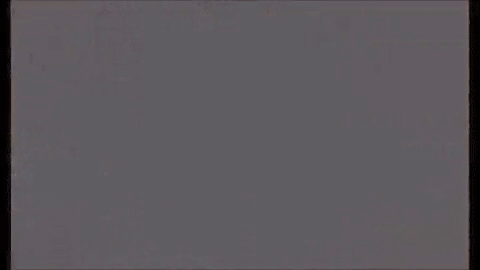
This meant that we only have to simulate the positive points (since the negative points are identical). This saves down the number of points by a factor of two for each extra dimension! Unfortunately, this wouldn’t quite get us to 10D, but the discovery completely changed how we saw this puzzle. With one breakthrough down, we began to believe that there would be more just around the corner, made possible by our problem’s special 2D-slice starting degeneracy.
Such a dream (as posed in this reddit thread I started) turned into a month-long ride of breakthrough after breakthrough, exploiting different aspects of this degeneracy. It was a month full of sudden twists and turns and bursts of excitement whenever new innovations came. And in the end, the hopeful question “7D is barely in reach; what if 10D was possible?” turned into “10D in 100ms, 40D in eight minutes…can we do 60D quickly?” This post even includes simulations to prove that we got 10D fast enough to run on easily on any modern browser. The whole journey became an adventure in the power of visualization combined with abstract thinking.
So, let’s take a deep dive — deeper than you probably ever expected to dive into any particular degenerate starting conditions of a hyper-dimensional game of life :D
There will be python code samples here and there, but just for context, my actual solvers I developed along the way were written in Haskell, and all of the solving logic embedded in this post was written in Purescript (online here) and compiled to Javascript.
Table of Figures
For reference, the interactive elements in this post are:
- Initial condition drawer
- 2D Game of Life
- 3D Game of Life
- 3D Forward Neighbor Multiplicities / 3D Reverse Neighbor Multiplicities
- 4D Game of Life
- 4D Forward Neighbor Multiplicities / 4D Reverse Neighbor Multiplicities
- 5D Neighbor Multiplicities
- General Neighbor Multiplicity Algorithm
- N-D Game of Life
Starting Off
First of all, let’s meet our friend for the rest of this journey. In the drawer below, you can draw (with your mouse) the 8x8 grid you want to simulate for the rest of this post. As you draw, the rest of the visualizations will update to use this as their initial conditions, so feel free to jump back and forth as you’re reading to customize and change what you want to simulate.
Element 1: Initial Condition Drawer
Please enable Javascript
Here are some sample fun ones you can try out (click to load):
- The classic glider, a default if only for how iconic it is.
- The tub, which is a “still-life” in 2D, but explodes into a twinkling frenzy during the 4D animation.
- The full block, which dies out in 2D but produces very appealing patterns in 3D and 4D. A bulls-eye also yields interesting “geometric” patterns at higher dimensions. A broken bar code also yields explosively intricate alternating behavior at higher dimensions.
- The spiral galaxy with rotational symmetry, which produces rich spiral galaxy patterns up until 6D, but then all of a sudden becomes blocky and bland at 7D and above.
- My own personal assigned puzzle input, to see what the typical input looks like that people had to run on December 17th.
I recommend trying out some of the other interesting well-known patterns from 2D GoL, as well! If you find any interesting ones, I would be excited to hear about them!
For fun, here’s a 2D vanilla game of life implementation (for six time steps) to test out your creation. Remember that some starting conditions will putter out in 2D, but expand forever in 3D+ due to the abundance of neighbors.
Element 2: 2D Game of Life
Please enable Javascript
Now that that’s there, let’s start at the beginning: what’s the naive, baseline solution?
A reasonable initial thought would be:
- Keep a 2D (or 3D, or 4D, etc.) array of booleans.
- At each step:
- Make a fresh copy of the entire space (\(O(n^d)\)).
- Loop over each item in your array (\(O(n^d)\)). Count all of the neighbors (\(O(3^d)\)) that are
true(“alive”), and write to the new array based on the rules table of GoL (2 or 3 neighbors for a live cell stays alive, 3 neighbors for a dead cell turns alive).
- You have a new array! Loop again six times.
Sounds reasonable enough! This does work for the 2D case pretty well (like in the Day 11 puzzle). However, there are some clear issues when moving into higher dimensions. The size of your array grows exponentially on your dimension, and so does the number of neighbors you’d have to check. And the curse of dimensionality assures us that more and more of that array would become wasted as the proportion of “on” points shrinks to zero for higher dimensions.
Oh, but what’s that? The percentage of “on” points shrinks to zero for higher dimensions? That actually sounds like something we can use to our advantage! The blessing of dimensionality*, I daresay? Because we know the vast majority of our points will be “off”, there’s another approach:
- Keep a set of points that are “on”.
- At each step:
Initialize a dynamic map (key-value store, like a python dict or Counter) of points to integers. This map associates each point to the number of live neighbors it has.
For each step, iterate over each of your “on” points, expand all of their neighbors \(n_i\) (\(O(3^d)\)), and increment the value associated with \(n_i\) in your dynamic map.
For example, if the point
<2,3>is in your set of live points, you would add increment the map’s values at keys<1,2>,<2,2>,<3,2>, etc.: all 8 neighbors of<2,3>.Collect your new set of “on” points: keep all of the keys in your dynamic map corresponding to live points if their integers are 2 or 3, and keep all of the keys in your dynamic map corresponding to dead points if their integers are 3.
- You have a new set! Loop again six times!
(I discuss this algorithm much more deeply with actual code in my solutions write-up in my Advent of Code reflections journal)
This method nets us a huge advantage because we now only have to loop over the number of items that we know are alive, and any points away from our set of alive points can be properly ignored. This narrows down our huge iteration space, and the benefits compound with every dimension due to the blessing of dimensionality.1
Both methods can be generalized to any dimension; in this second method, this just means a different sized tuple/vector in your set of alive points ([x,y] vs. [x,y,z]). One extra concern, though, is that you need to think through generating all \(3^d-1\) neighbors: that’s going to come down to a d-ary cartesian product of [-1,0,1] to itself.
Here’s a python implementation of the set-based method, using a nice trick I learned from phaazon and glguy to get the right neighbors by doing a cartesian product against [0,-1,1] instead of [-1,0,1], which leaves the first item as the <0,0> “original point” we want to exclude.2
from itertools import islice, product
from collections import Counter
def mk_neighbs(point):
"""Return neighboring points, with the original point first
(1, 2)
=> [(1, 2), (1, 1), (1, 3), (0, 2), (0, 1), (0, 3), (2, 2), (2, 1), (2, 3)]
"""
return list(product(*[[x, x-1, x+1] for x in point]))
def step_naive(pts):
"""Takes a set of points (tuples) and steps them in the simulation
"""
neighbs = Counter()
for point in pts:
# skip the first item, the original point
neighbs += Counter(mk_neighbs(point)[1:])
def validate(point, ncount):
if point in pts:
return ncount == 2 or ncount == 3
else:
return ncount == 3
return frozenset(p for p, n in neighbs.items() if validate(p, n))Three Dimensions
Let’s see how this looks for the 3D case! To make things easier to see, we can render things in “slices” in 3D space: each grid represents a slice at a different z level (ie, the z=0 square represents all squares <x,y,0>, the z=1 square represents all squares <x,y,1>, etc.). Press “Play” to have the simulation cycle through 6 time steps!
Element 3: 3D Game of Life
Please enable Javascript
(Some patterns I suggest trying out are the flowery spiral galaxy pattern and patterns with a single reflection symmetry, like the broken bar code; double symmetry like bulls-eye look nice too!)
In reality, each of those 13 slices above are stacked on top of each other in 3D space. You’ll see that your live cells spread out from the center z=0 slice, which means they are actually spreading “up and down” the z axis.
If you mouse over (or tap) any individual tiny <x,y> cell, you’ll see the all of the 26 (\(3^d-1\)) <x,y,z> 3D neighbors of the point you’re hovering over highlighted in blue — these 26 points form a 3D cube around your mouse through the stacked slices. You can use this cube to help see how the simulation progresses. If your mouse is hovering over a live cell, and there are 2 or 3 live cells highlighted in your cube, it’ll stay alive in the next time step. If your mouse is hovering over a dead cell and there are exactly 3 live cells highlighted in your cube, it will come alive in the next step.
Axis Reflection Symmetry
Try playing around with different initial conditions to see how they evolve! See any patterns?
Freenode IRC user sim642 noticed something late into the night of December 16th:
I wanted to ask this before but forgot: did anyone try to take advantage of the symmetry, e.g. in z axis in part 1? Should halve the amount of calculations you have to do.
Only some extra work at the end to differentiate z=0 and z>0 positions to know which to count twice And in part 2 I feel like you could also exploit the symmetry in w axis simultaneously
— sim642
You might have seen this too: the entire thing has reflection symmetry across z=0! z=1 is always the same as z=-1, z=2 is always the same as z=-2, etc. Fundamentally, this is because our starting solution has a z-axis symmetry: the initial 2D slice is symmetric with reflections across z, because z=0 for all of those points. This is the first “degeneracy” that this blog post’s title is referring to: the negative and positive directions are interchangeable! This is reflected in the yellow highlight on hover: when you mouse-over a z square, its corresponding reflected twin is highlighted, and will always be identical.
This means that we actually only need to simulate positive z’s…and for our final answer we just “un-reflect” to get the total number.
Let’s do this! Apparently, the picture is slightly more complicated than simply halving the points; we also need to change how to distribute neighbors. That’s because, once we commit to only keeping the positive z’s, some cells need to be double-counted as neighbors. In particular, any z=0 cell would previously had a neighbor at both z=-1 and z=1…but now if we only keep the positive z’s, it would have z=1 as a neighbor twice.
The following interactive element lets you explore what this looks like:
Element 4a: 3D Forward Neighbor Multiplicities
Please enable Javascript
Each square represents an entire “slice” of z. When you mouse-over or tap a z-cell, its z-neighbors are highlighted with how many times that neighbor has to be counted, and the green bar tells you from what direction that neighborship arose from. For example, mousing over z=3, you will see z=2 and z=4 get highlighted with the values “1” because they are neighbors of 3, on the left and right side (respectively). Note that one neat property for all squares (except for z=6, which goes off the scale) is that the “total” higher-dimensional neighbors is always 2 (\(3^{d-2}-1\)) just like before; it’s just that where those neighbors fall is re-arranged slightly.
The tricky square is now z=0: if you mouse-over it, you’ll see that it has a single neighbor z=1 that is counted twice, as a neighbor from both the left and right side.
We can compute the above diagram by expanding any z to its neighbors (z-1, and z+1), applying the absolute value function, and seeing how points double-up. This gives us the forward neighbors, and we can directly use it for the original “keep the full array” GoL implementation method.
However, for the “keep active points and expand their neighbors” GoL implementation, we have to find the opposite of this. Remember that to build our “neighbors map” (the map of points to how many active neighbors they have), we have each cell “proactively” add its contributions to all of its neighbors. <1,2,3> is a neighbor to <1,3,4> once, so when we expand <1,2,3> we would increment the value in the map at <1,3,4> by 1 because <1,2,3> is a neighbor of <1,3,4> once.
So the question becomes: how do we count <1,3,1> expanding into <1,3,0>? Well, normally, <1,3,1> is a neighbor of <1,3,0> once. However, if we only keep the normalized z values, <1,3,1> is a neighbor of <1,3,0>…twice! To compute the total neighbor count of <1,3,0>, we have to count the contribution from <1,3,1> twice (once for <1,3,1> and once for <1,3,-1>, which also exists, but was normalized away).
That means we have to follow the original rules, but backwards, like:
Element 4b: 3D Reverse Neighbor Multiplicities
Please enable Javascript
These are the reverse neighbors: how many times a given point counts as a neighbor for its surrounding points. Here, mousing over z=1 shows that it counts as a neighbor for z=0 twice, from both the left and the right. It also counts as a neighbor for z=2 once (from the left side).
We can account for this by hard-coding the rules into our step algorithm: if our z goes from 1 to 0, increment its value twice in the neighbor map. Otherwise, simply increment by 1 as normal.
This rule is relatively straightforward to implement, and as a result we now halved our total number of points we need to keep and check for 3D! There’s also a nice way to generalize to arbitrary dimensions: for every 1 -> 0 transition in a higher dimension, multiply by two. That means we reduce the number of 4D points we need to track by a factor of four, the number of 5D points by a factor of eight, the number of 6D points by a factor of 16… now our total points to check only grows as \(O(n^d / 2^{d-2})\) instead of \(O(n^d)\)!
Here is a python implementation of this generalization:
def axis_weight(source,target):
"""Retuns how many times the given source->target transition should be
counted in target's neighbor count
"""
# ignore x,y
higher_source = source[2:]
higher_target = target[2:]
return 2**sum([1 for i,j in zip(higher_source, higher_target)
if i == 1 and j == 0
])
def mk_positive_neighbs(point):
"""mk_neighbs, but only with positive higher dimensional points
"""
# this is a very wasteful implementation, for demonstrative purposes
return [ngb for ngb in mk_neighbs(point) if all (i >= 0 for i in ngb[2:])]
def step_axis(pts):
"""Takes a set of points (tuples) and steps them in the simulation
according to axis-reflection symmetry.
"""
neighbs = Counter()
for point in pts:
neighbs += Counter({ ngb: axis_weight(point,ngb)
for ngb in mk_positive_neighbs(point)[1:]
})
def validate(point, ncount):
if point in pts:
return ncount == 2 or ncount == 3
else:
return ncount == 3
return frozenset(p for p, n in neighbs.items() if validate(p, n))This discovery late in the Tuesday night of the 16th was what inspired us to believe and dream that more breakthroughs might be possible to bring things down even further.
Those breakthroughs soon came!
Four Dimensions
Let’s look at how 4D game works! We can visualize this by taking “z-w” slices at different x-y planes. The labels in the following boxes are the <z,w> of each slice. The very center is <z,w> = <0,0> the row in the middle from the top is w=0, and the column in the very middle from the left is z=0. It’s basically taking the 3D visualization above and expanding it in an extra dimension. Press “Play” to run your initial conditions!
Element 5: 4D Game of Life
Please enable Javascript
(Some patterns I recommend trying are the patterns with double reflection symmetry like bulls-eye, full block and the twinkly tub, rotational symmetry like spiral galaxy, and single-reflection symmetries like broken bar code, which seems to alternate between different orientations).
Most initial conditions will spread out from the center <z,w> = <0,0> slice radially, spreading outwards into positive and negative z and w. Mouse-over or tap any individual tiny <x,y> cell and you’ll see each of its 80 (\(3^4-1\)) <x,y,z,w> 4D neighbors highlighted in blue, forming a little 3x3x3x3 “tesseract” (4D cube, or hypercube). Like in the 3D case, you can use this little hypercube to track how the simulation progresses: if your mouse if hovering over a live cell with 2 or 3 live cells in its hypercube, it’ll stay alive in the next step, if it’s hovering over a dead cell with 3 live cells in its hypercube, it’ll come alive in the next step.
Diagonal Reflection Symmetry
Play around and explore how simulations evolve! You will notice that the axis reflection symmetry is still preserved, as expected, but four ways (the slice at <z,w> = <3,4> is always going to be identical to the slice at <-3,4>, <3,-4>, and <-3,-4>). These are reflected in the “deep yellow” highlights above when you mouse over a zw square. (Ignore the lighter yellow highlights for now!)
And now, for the next big breakthrough: this exact visualization was what reddit user u/cetttbycett was looking at when they made this post late Thursday the 17th/early Friday the 18th…and everything changed forever.
I noticed that the expansion of active cubes for part 2 is symmetric with respect to two hyperplanes in 4d space: These hyperplanes can be described by w = 0 and w-z = 0.
Using these symmetries could make the code nearly eight times as fast.I was wondering if anyone tried that.
— u/cetttbycettt
What u/cetttbycettt saw is what you can see now in the simulation above: it’s all of the light yellow highlighted squares when you mouse-over (highlighting even more identical slices to the one you are hovering over). In addition to the z=0 and w=0 lines (the two lines down the middle, up-down and left-right), we also have another line of symmetry: z=w and z=-w, the diagonal lines!
That’s right, a zw slice at <z,w>=<3,4> is identical to the one at <4,3>, and so also <-3,4>, <3,-4>, <-3,-4>, <-4,3>, <4,-3>, and <-4,-3>! Each slice is potentially repeated eight times! The exceptions are the points on the lines of symmetry themselves, which are each repeated only four times, and also <z,w>=<0,0>, which is in a class of its own.
So, our first breakthrough meant that we only have to simulate positive coordinates (a single quadrant)…our next breakthrough means that we only have to simulate coordinates on a single “wedge” half-quadrant…and then duplicate those eight times at the end. (Arbitrarily, let’s say we only simulate the north-by-northeast wedge, because it’s easy to normalize/compact all points onto that wedge — you just need to absolute-value all the components and sort them, and a point like <4,-3> gets “normalized” to <3,4>))
We found a new symmetry now, but we run into the same issue as before: How do we propagate neighbors? To help us see what’s going on, let’s look at the map of neighbors between different <z,w> squares, for the single zw wedge we are simulating.
Element 6a: 4D Forward Neighbor Multiplicities
Please enable Javascript
These are the forward neighbors; we can compute them by expanding a point to its neighbors, and then normalizing our points and seeing how they double (or quadruple) up.
For example, mouse over <z,w>=<3,3> and see it has eight total higher-dimensional neighbors (like all points should, though this visualization leaves out points at w>6). It’s supposed to have a neighbor at <4,3>, but that gets reflected back onto <3,4> during our normalization process, so you see that the point <3,3> has a neighbor at <3,4> “double-counted”. The green squares (in the north and west positions) at <3,4> when you hover over <3,3> show that <3,4> is a neighbor of <3,3> both to its north and to its west.
Also, we have something really odd show up for the first time. Mouse over a point like <z,w>=<2,3> and see that it has a neighbor in…itself? What’s going on here? Well, it is supposed to have a neighbor at <3,2> but that gets normalized/reflected back onto <2,3> — it reflects onto itself! The green square in the Southeast means that <2,3>’s southeast neighbor is…itself!
Here is a sample python implementation of the computation of forward neighbor multiplicities for any dimension by propagating-then-normalizing:
def normalize(point):
"""Normalize a point by sorting the absolute values
(2, -1)
=> (1, 2)
"""
return tuple(sorted([abs(x) for x in point]))
def forward_neighbs(point):
"""Generate the higher-dimensional forward neighbors of a point
(0, 1)
=> {(0, 1): 2, (1, 2): 2, (1, 1): 2, (0, 0): 1, (0, 2): 1}
"""
return Counter([normalize(neighb) for neighb in mk_neighbs(point)[1:]])The forward neighbors are useful for understanding what’s going on, but to actually run our simulation we again need to find the reverse neighbors: from a given point A, how many times is that point a neighbor of another point B?
We can compute this in brute-force using a cache: iterate over each point, expand all its neighbors \(a_i\), normalize that neighbor, and then set \(a_i\) in the cache to the multiplicity after normalization.
def reverse_neighbs_table(t_max):
"""Tabulate the reverse neighbors of all zw slices reachable before t_max
"""
weights = {}
for i in range(t_max):
for j in range(i, t_max):
for neighb, ncount in forward_neighbs((i, j)).items():
if neighb in weights:
weights[neighb][(i, j)] = ncount
else:
weights[neighb] = {(i, j): ncount}
return weightsThis seems pretty expensive and wasteful, so we’d like to maybe find a formula to be able to do this using mathematical operations. So, let’s explore!
Element 6b: 4D Reverse Neighbor Multiplicities
Please enable Javascript
These are the reverse neighbors, and it follows the same rules for the 3D Reverse Neighbors: mouse over a point and you’ll see how many times it appears as a neighbor to its nearby points. The green square represents the direction that it sees the hovered point as a neighbor. It’s the flipped version of the 4D Forward Neighbors above.
After exploring this interactively, we can maybe think of some rules we can apply.
- If we have a point
<z,z>directly on the z=w diagonal, just use its five normal left/up neighbors with weight 1 each. - If we have a point
<z,z+1>on the “inner-er” diagonal, use its five normal left/up neighbors with weight 1, but its south and west neighbors have weight 2, and the point reflects onto itself with weight 1. - If we’re on
z=1and we move intoz=0, double that count (phew, the same rule as in the 3D case earlier) - If we’re on w=1 and we move into w=0, double that count (same as before)
- And…I guess
<0,1>reflects onto itself twice? I guess that technically falls under a combination of rule 2 and rule 4, but we don’t directly observe the motion into w=0 before it gets reflected so it has to be special-cased.
Okay, those rules are sliiightly more complicated than our 3D rules (“if we go from z=1 to z=0, double-count it”)…but they’re at least mechanical enough to code in, even if not beautiful. You can probably foresee that it might be tough to generalize, but…we’ll tackle that when we get there :)
For now, we have a super-fast implementation of 4D GoL with our special degeneracy! The runtime gets reduced by a factor of 8!
For clarity, here’s an example implementation of how we can do this higher-dimensional wrangling:
def reverse_neighbs(point):
"""Return normalized higher-dimensional points, with their reverse
multiplicities
(0, 1)
=> {(0, 0): 4, (0, 1): 2, (1, 1): 2, (0, 2): 1, (1, 2): 1}
"""
# implementation elided
# one possibility is to lookup into reverse_neighbs_table(t_max)[point]
return {}
def step_with_weights(pts):
neighbs = Counter()
for point in pts:
# 2d component, <x,y>
pt_2d = point[:2]
# higher-dimension components, <z,w,...>
pt_nd = point[2:]
# insert neighbors in the same 2d slice, not including itself
neighbs += Counter([ngb + pt_nd for ngb in mk_neighbs(pt_2d)[1:]])
# insert neighbors in the neighboring 2d slices
neighbs += Counter({(ngb_2 + ngb_n): wt
for ngb_n, wt in reverse_neighbs(pt_nd)
for ngb_2 in mk_neighbs(pt_2d)
})
def validate(point, ncount):
if point in pts:
return ncount == 2 or ncount == 3
else:
return ncount == 3
return frozenset(p for p, n in neighbs.items() if validate(p, n))Now, onward to 5D!
Breaking Through
By stepping into 5D, we’ve moved into a brand new territory — we’re now past what the original question was asking about, and into simply exploring a personal curiosity for fun. No longer are we “super-optimizing” the puzzle — we’re now warping the original challenge to levels it was never designed to handle.
It’s difficult to visualize how things look in 5 dimensions, so this is where it gets a little tricky to make any progress, mentally. The first thing we need to figure out is how exactly we can generalize the “z=w” symmetry from 4D to be able to take advantage of it in 5D…and hopefully in a way that can generalize to arbitrary dimensions. Along the way we’d also like to get rid of our hacky 4D neighbor multiplicity rules and get something a little cleaner.
I struggled with for a while without making too much headway…but on the morning of Friday, December 18th, arguably the biggest revelation of the entire journey was dropped by Michal Marsalek on u/cetttbycettt’s reddit thread. It was a big deal, because not only did it allow us to generalize our symmetries to higher dimensions, but it also proved a specific degeneracy that allowed 10D simulation to be definitely 100% solvable.
Permutation Symmetry
Here was Michal’s historic post:
Yes, all the higher dimensions are interchangeable, there’s nothing that distinquishes them. That is, if there’s an active cell at position (x,y, a,b,c,d,e,f,g) then, there’s also one at (x,y, c,d,g,e,f,a) and at all other permutations, of coordinates a-g). That is the number of cells that one need to track can be reduced by factor of \((d-2)! \times 2^{d-2}\) (at least if time goes to infinity).
…we can use symmetries coming from permutations, to only track cells where \(0 \leq x_2 \leq x_3 \leq\,\ldots\, \leq x_{d-1} \leq t\). There’s \(20^2 \times \sum_{k=0}^{t} { {d-3+k} \choose {k} }\) such cells.
— Michal Marsalek
(equations slightly modified)
And boy was this exciting to read. First of all, it gave a way to generalize the z=w symmetry: it’s just permutation symmetry for all higher-dimensional coordinates! But the big kicker here: See that last formula? Let’s look at it more closely, using \(\hat{d}\) to represent \(d-2\), the number of higher dimensions:
\[ 20^2 \times \sum_{k=0}^{t} { {\hat{d}-1+k}\choose{k} } \]
(That notation is the binomial coefficient, if you aren’t familiar with it.) Note that the summation has a fixed number of terms (with respect to dimension); that means we only ever have 6 terms to expand, no matter how high the dimensions are — at 10D and even 100D! Furthermore, we can simplify the above using properties of binomial coefficients to get
\[ 20^2 \times { {\hat{d}+6}\choose{6} } \]
This binomial coefficient is actually polynomial on \(\hat{d}\) — it’s \(\frac{1}{6!} \prod_{k=1}^6 (\hat{d}+k)\) — a sixth degree polynomial (leading term \(\frac{1}{6!} \hat{d}^6\)), in fact. This means that we have turned the number of points we potentially need to track from exponential (\(O(13^{\hat{d}})\)) to slightly smaller exponential (\(O(6^{\hat{d}})\)) to now polynomial (\(O(\hat{d}^6)\))!
So, not only did we figure out a way to generalize/compute our symmetries, we also now know that this method lets us keep our point set polynomial on the dimension, instead of exponential.
To put a concrete number for context, for that dream of 10D, here are only \({ {8+6} \choose 6 }\), or 3003 potential unique <z,w,...> points, once you factor out symmetries! The number went down from \(13^8\) (815,730,721) potential unique <z,w,...> points to \(6^8\) (1,679,616) potential unique points with positive/negative symmetry to just 3003 with permutation symmetry.3 Furthermore, because of the blessing of dimensionality mentioned earlier, we can expect more and more of those to be empty as we increase our dimensions.
And in a flash, 10D didn’t feel like a dream anymore; it felt like an inevitability. And now, it was just a race to see who could get there first.
The Race to 10D
Unfortunately, the exact record of who reached and posted 10D first is a bit lost to history due to reddit’s editing records (not that “first” is necessarily a meaningful title to hold; there’s no prize, and everyone is working at their own pace). A few people maintained and updated their posts to prevent clutter, but the record and time stamp of when they first posted 10D is lost. If any of them happens to read this and can more accurately verify their times, I’d be happy to update!
For me, I’m sure I was not the first one, but in my chat logs I see that I chimed into freenode’s ##adventofcode-spoilers channel in excitement in the wee morning hours (PST) Saturday December 19th:
2020-12-19 02:32:42 jle` | d=10 in 9m58s
2020-12-19 02:33:05 jle` | hooray my goal :)
2020-12-19 02:33:08 jle` | time to sleep now
2020-12-19 02:33:12 xerox_ | goodnight
2020-12-19 02:33:35 jle` | xerox_: thanks :)Pure joy! :D
Peter Tseng made a post on Thursday night with times, but I can’t remember if it incorporated all the symmetries or originally included 10D. Michal Marsalek was able to implement the idea that he originally proposed by the following Wednesday (December 23rd) in Nim to blow everyone’s time out of the water: 3 seconds flat!
At that point, it was pretty unbelievable to me that what started out as a dream goal that we couldn’t have reasonably completed on a commercial PC had, through successive revelations and insights building on each other one by one, could now be done in 3 seconds.
But hey, I promised 100ms in the introduction, and a way to reach 60D, right?
With our original goal completed, it was now time to dig in a little deeper and see how far this baby could go.
Diving Deeper: Terminology
Before we go any further, let’s take a break to clarify and introduce some terminology we’ll be using for the rest of this post.
I’ve been using the word slice to talk about a 2D grid representing a single higher-dimensional
<z,w...>coordinate — they’re the 13 grids in the 3D simulation and the 169 grids in the 4D simulation.I’ve also been using cell to refer to an exact specific
<x,y,z,w,..>spot — they are the tiny squares inside each grid in the simulations above.I’ll start using the word coset to refer the set of all of the duplicates of an
<x,y>across all permutations and negations of<z,w,q,..>, since they all behave the same (they are either all on or all off together). So<x,y,1,2>,<x,y,2,1>,<x,y,-1,2>,<x,y,1,-2>,<x,y,-1,-2>,<x,y,-2,1>,<x,y,2,-1>, and<x,y,-2,-1>are all a part of the same coset, represented by the normalized form<x,y,1,2>. Now, during our simulation, we only need to simulate one member from each coset, because every member is identically present or not present. For the sake of implementation, we simulate the arbitrary normalized (positive and sorted) member only. Because of this, we’ll sometimes refer to the normalized item and the coset it represents as the same thing.I’ll also start using slice coset to talk about the set of all
<z,w,...>slices) across its permutations and negations. The slices at z-w coordinates of<1,2>,<2,1>,<-1,2>,<1,-2>,<-1,-2>,<-2,1>,<2,-1>, and<-2,-1>are all a part of the same slice coset, represented by the normalized form<1,2>. All of the slices at each of those zw coordinates will always be identical, so we can talk the state of a single slice at<1,2>as representing the state of its entire coset.Slice cosets are what are being highlighted on mouseovers for the 3D and 4D simulations. They are also what the big squares represent for the 3D Forward Neighbors, the 3D Reverse Neighbors, the 4D Reverse Neighbors, and the 4D Reverse neighbors elements: each slice stands in for their entire slice coset, and we show the amount of times each normalized slice coset element is a neighbor of the other.
Tackling the Neighbor Problem
My initial d=10 time clocked in at just under 10 minutes initially, but as early as next Wednesday we knew that a sub-5 second time was possible. So where was the gap?
Well, I didn’t really know what to do about the neighbor multiplicity problem. I was still brute-forcing by way of forward neighbors + normalizing (as in the sample 4D python code snippet earlier). The naive brute-force method requires computing all \(3^{ {\hat{d}} } - 1\) higher-dimensional neighbors. So, even though the number of points I’d have to track grows polynomially, I still had that pesky exponential factor in building my neighbor cache. At high dimensions, that exponential factor dominates over everything.
So put on your hard hats and working boots … we’re going to dive deep into the world of hyper-dimensional symmetries!
Five Dimensions
First, let’s start visualizing how things look like in 5 dimensions, now that we know what our slice coset/representative structure looks like. Partially to help us gain an intuition for some of what’s going on, and also partially to show that intuition at the individual component level can only get so far.
It’s a bit difficult to duplicate the same forward neighbor/reverse neighbor interactive elements as we had for 4D, so here’s a different representation. Here is an interactive element of all of the <z,w,q> slice cosets (the wedge of normalized points we track for our implementation) and both their forward and reverse neighbor weights of each other (computable using the method we used for 4D). The q axis is represented as stacked zw sections from left to right.
Element 7: 5D Neighbor Multiplicities
Please enable Javascript
As you mouse-over a slice coset representative (a single square), all of its neighbors will be highlighted, including reflections. The red dot on the left is the forward neighbor multiplicity (how many times that other slice is a neighbor of the hovered slice) and the blue dot on the left is the reverse neighbor multiplicity (how many times the hovered slice is a neighbor of the other slice). For example, if you hover over <z,w,q>=<1,3,4>, you can see that <0,3,4> is its neighbor twice, and <1,3,4> is <0,3,4>’s neighbor four times. These four times come from the normalized reflections of <1,3,4> at <1,3,4>, <1,4,3>, <-1,3,4>, and <-1,4,3>. Some squares are also neighbors to themselves (like <1,4,5>, which reflects off of the top edge at <1,5,4>) and some are not (like <1,3,5>). Mind bottling!
At least one pattern we can see clearly is that if you are at a point where each component is 4 or lower (so it doesn’t run off the edge of our table), the sum of all its neighbors’ red dots (the forward neighbors) is \(3^3-1\) = 26, just like how the sum of forward neighbors for interior points in 3D is \(3^2-1\) = 8, and for 2D is \(3^1-1\) = 2.
Another very important pattern is that “is a neighbor” seems to be reversible: the set of all forward neighbors of a point is the same as all reverse neighbors of a point — the only difference is the multiplicities. That is, wherever you see a red dot, you will also always see a blue dot. No single-dot squares.
Anyway, you can explore this a little bit and try to come up with a set of ad-hoc rules like we did for 4D, but I think we’ve reached the limits of how far that method can go. We can generate these values simply enough using the expand-normalize-tabulate method we did for 4D, but it’s pretty inefficient, and there should be a way to compute these weights directly in a clean fashion that doesn’t require hard-coding special cases and patterns. It’s clear that we are limited until we can find this method.
Go with the Flow
What do all our valid normalized <z,w,...> coordinates look like? Well, they are always non-decreasing, and always are less than or equal to the current timestep. Keeping t=6 as our goal still, this means that valid coordinates in 10D are strings of eight numbers, like 0,1,1,1,3,5,5,6, or 0,0,3,4,4,4,6,6, or 1,1,2,3,3,4,5,5.4
We run into problems working with this format, though. For example, if we’re computing a neighbor of 0,1,1,1,3,5,5,6, we can imagine that the very first 1 (the w coordinate) could move to be a 2, resulting in 0,2,1,1,3,5,5,6. However, we’re now in un-normalized territory…we have to re-sort it to turn it into 0,1,1,2,3,5,5,6. This encoding isn’t something we can directly manipulate in a nice way.
Because we don’t care about order, what if we instead encoded each higher-dimensional coordinate as “count of each value seen?” For example, we can encode 0,1,1,1,3,5,5,6 as 1-3-0-1-0-2-1: the first slot represents how many 0s we have, the second how many 1s, the next how many 2s, the next how many 3s, etc. We can encode 0,0,3,4,4,4,6,6 as 2-0-0-1-3-0-2 and 1,1,2,3,3,4,5,5 as 0-2-1-2-1-2-0. The sum of the components gives you the total number of higher dimensions (ie, 10D vectors sum to 8)
And now, a “valid transition” becomes easy to enforce: it’s an amount “flowing” from one of those bins to another. For example, turning a 1 into a 2 in 1-3-0-1-0-2-1 turns it into 1-2-1-1-0-2-1. We took one of the three 1s and turned them into a single 2. This “flowing” operation automatically gives us a valid coordinate without any re-normalizing necessary!
In this light, we now have an algorithm to compute neighbors without requiring re-normalization: we can walk bin-to-bin, “flowing” components from our origin vector to our new vector. We no longer have to try all \(3^d-1\) (exponential) candidates and re-normalize: we can now only iterate through the ones we care about.
The tricky math is now in computing the multiplicities. Interestingly enough, in this case, the reverse direction is actually easier to conceptualize than the forward direction. Good for us, because that’s the direction we actually need!
Let’s imagine we start at 0-2-1-3-0 (1,1,2,3,3,3) and “flow” to 0-0-5-0-0 (2,2,2,2,2) by dumping all our bins into 2. How many ways could this flow happen? The answer happens to be the multinomial coefficient \(5 \choose
{2,1,3}\) (or \(5! / (2!\,1!\,3!)\)): there are 5! ways to end up with 5 in the bin, but that 5 came from contributions of 2+1+3 from either side, and so we divide by the ways we could pick from those contributing bins (2!, 1!, and 3!).
Finally, we have to treat multiplicities for transitions from 0 to 1 slightly differently, because they can arise either a 0 to 1 transition or a 0 to -1 transition. This comes out to a multiplication of \(2^n\) at the end (n being the amount of 0-to-1 flow). Because of this special care, it’s actually more convenient to fill in bin-by-bin “backwards”, from the 6 slot to the 5 slot to the 4 slot, etc., because your options at the 0 component are already pre-determined for you by the choices you have already made. It keeps the tree a more manageable shape.
Alright, enough words, let’s look at this in action! The following element shows the tree describing all the ways you can flow from bin to bin. As an example, let’s look the 6D case of ways each point is a neighbor of 0,2,2,3 (1-0-2-1), which you can pick from the drop-down.
Element 8: General Neighbor Multiplicity Algorithm
Please enable Javascript
As you can see, each “branch” in the tree (reading from left to right) is a different way to fill in a given bin, from right to left. At each node, the displayed upper vector is the “source” vector, and the lower vector is the “target” vector we build bin-by-bin. Bin-by-bin, we begin to move components from our source vector into our target vector. The branches in the tree reflects different ways we can commit a bin in our target vector. For example, at the very first split, we can either pick our final vector to be ?-?-?-?-0 (leaving that 3 bin alone) or ?-?-?-?-1 (swiping a component from that 3 bin in the source vector). The operation shown to the right of the node represents how we modify our weights according to the choices we make according to the logic above. The nodes on the far right also show the end products: the actual neighbors, along with their multiplicities.
If you mouse-over or tap a node, it’ll highlight the trace from the beginning to the node you are highlighting, so you can see all of the choices made, as well as all the operations applied to our running multiplicity counter at each step. It’ll also show the contributions from the left, center, and right of the current bin being picked (the \(2+1+3\) in the example above), and also the “regular” vector representation. For example, <[2,2],2,4> means that that node has already committed to having <?,?,2,4> in the target vector, but still has two 2s in the source vector to pull in and distribute.
One final thing we need to keep track of is to not count a point transitioning to itself if it results from no actual internal changes (this is the “minus one” in \(3^d-1\): we should not include the single original point itself, but we should count extra occurrences of the original point if it arose from a reflection). This can be done by checking if each of our bin choices involved exactly no inter-bin flows (they were all of the form 0+x+0).
Phew! That’s a bit of a mathematical doozy, huh? But trust me when I say it’s easier to understand if play around with the interactive element and follow along the traces. After a few examples in different dimensions, it might start to make sense. Try looking at the lower dimensions too to see if they match up with what we figured out before.
You can also flip the switch on the element to compute reverse and forward neighbors. Luckily, as we noted before, if a point is a forward neighbor, it is also a reverse neighbor. This means that the branching structure for forward and reverse neighbor trees are exactly the same; the only difference is how the multiplicities are calculated. In this case, the forward direction is just the original calculation “reversed”! The diagram shows how the multiplicities are accumulated; feel free to try to work out exactly how this works as a fun exercise :)
And with that, we have tackled the reverse neighbor weights problem with some branching bin flows and combinatorics!
Stacks On Stacks: Visualizing Arbitrary Dimensions
You might have noticed that ever since our 4D simulation, we haven’t had a new visualization of simulation, despite now having higher dimensions in our grasp. Why not?
Well, there’s the question of how you might even visualize this. You can “zoom out” and take higher-dimensional slices of our 4D visualization and repeat this ad nauseam, but that doesn’t really add anything or give any insight as to what’s really going on.
I believe that this is one of the things that caused us to all collectively get “stuck” together around 20 dimensions. The rush of the revelations one after within a single week pushed us into trying many different things. I had a couple of dead-end forays into pre-cacheing and had a lot of code (that I was ecstatic to be able to later delete) working with an sqlite3 database.5
Another factor that probably contributed to the overall lull was that Advent of Code was still running, and we all still enjoyed doing the new puzzles every day. But soon, Christmas passed, the daily rush of doing new puzzles faded, and we started to return back to tinkering on this hyper-dimensional game of life puzzle. It wouldn’t be until January 1st, 2021 (just over two weeks after the puzzle originally came out) that a new revelation arose that would pave the way shoot far past 20D.
It was Michal Marsalek’s coset counts post that set the stage. From the beginning, he had always tracked the number of cell cosets at the end of the simulation (the number of active “normalized” cells), and had been exploring the relationship between dimension and coset counts. The discovery was that after a certain “saturation point” (6D for Michal’s set, 9D for Peter’s set, 7D for my set), all of the coset counts were perfectly quadratic! For mine, it followed the relationship \(d^2 + 109d + 70\) exactly for 7D and higher.
My best guess as to why this was happening is that, at 7D and above, we enter a domain of points where, before t=6, every point is at some sort of reflective boundary. Remember that even for 4D, we had really odd behavior at the reflective boundaries/edge of the wedge. There wasn’t enough room for many points to “stretch their wings” — every single one is at one reflective boundary or another. Being a boundary point corresponds to having a “bins” encoding with any bin greater than one or anything in the 0 bin (ie, 1-0-0-0 and 0-2-0 are all points on a reflective boundary).
Unfortunately, having a closed-form way to compute coset counts doesn’t actually give us a way to compute the final state itself (that we know of, yet), since it doesn’t tell us which cosets are active, just how many. However, this prompted me to investigate a little bit more about what was causing this pattern and how these cosets were distributed. To do this, I tried a new way to visualize things.
In our simulation, x and y components are fundamentally different from the others; we could actually talk about each point as a tuple (<x,y>, {higher dims}). Also, points are usually dense in <x,y> (a significant fraction of the xy space has at least one point), but sparse in higher dimensions (a very small fraction of the higher-dimensional space actually has a point in it). Instead of keeping our active points as a set of cosets, we could treat it as a map of <x,y> points to the higher-dimension slice cosets that live “under them”. That is, instead of keeping one giant set as:
{<1,2,1,1,3>, <3,1,1,1,4>, <1,2,0,0,5>, <4,2,3,4,4>, <3,1,2,2,2>}we could instead keep a map of sets:
<1,2>: { <1,1,3>, <0,0,5> }
<3,1>: { <1,1,4>, <2,2,2> }
<4,2>: { <3,3,4> }and propagate that in our simulation. I like to call those sets under each 2d point (ie, the {<1,1,3>, <0,0,5>}) a “coset stack”.
I did this initially to investigate the nature of the cosets that were showing up, but once I plotted it and animated things, I realized that in doing this, we are reducing the entire hyper-dimensional problem back to a variant of 2D cellular automaton! This whole thing becomes reframed…instead of a mind-bending hyper-dimensional deal, it’s now simply multivalued 2D cellular automaton with funky rules! It’s like a normal 2D game of life, but with funky rules for 2D points spreading to each other.
def step_with_stacks(stacks):
neighbs = {}
for pt_2d, pt_stack in stacks.items():
# higher-dimension components
for pt_nd in pt_stack:
rev_neighbs = Counter(reverse_neighbs(pt_nd))
rev_neighbs_incl_self = rev_neighbs + Counter(pt_nd)
# the actual propagation
# 1. add in the same stack; don't include self
if pt_2d in neighbs:
neighbs[pt_2d] += rev_neighbs
else:
neighbs[pt_2d] = rev_neighbs
# 2. add to nieghboring stacks; include self
for ngb_2 in mk_neighbs(pt_2d)[1:]:
if ngb_2 in neighbs:
neighbs[ngb_2] += rev_neighbs_incl_self
else:
neighbs[ngb_2] = rev_neighbs_incl_self
def validate(pt_2d, pt_nd, ncount):
if pt_nd in stacks[pt_2d]:
return ncount == 2 or ncount == 3
else:
return ncount == 3
return {pt_2d: frozenset(
pt_nd for pt_nd, n in pt_counts.items()
if validate(pt_2d, pt_nd, n)
)
for pt_2d, pt_counts in neighbs
}Here is the final animation: we plot a single 2D grid, and each cell is colored according to the size of the coset stack under that point (how many points exist with that <x,y>). You can slide this one up all the way to 10D to simulate it in your browser!
Element 9: N-D Game of Life
Please enable Javascript
(A lot of examples with symmetries look nice here, such as spiral galaxy up to 6D and bulls-eye; the alternating symmetries of broken bar code look nice too! But honestly, at higher-dimensions, almost any input ends up generating appealing gradients, like glider and my own assigned input)
Play around with it, it’s the big finale! :D You can move all the way up to 10D; some older devices may struggle, but on my lower-end cell phone it seems to run in less than a second. If you mouse-over a cell, the text box will show all of the slice cosets where that xy cell is alive in (the “coset stack”). If you click on a cell, your selection will “lock” on that <x,y> coordinate as you change dimensions and time.
Some interesting things you might notice:
At t=6, it looks like 8D, 9D, 10D (and sometimes 6D,7D) all have the same exact 2D cells “on”. They’re identical except for slightly different stacks above each of those cells.
To see this clearly, set your time to t=6 and drag your dimension slider back and forth to see all of the higher-dimensions look identical in shape.
This probably has something to do with the saturation theory I mentioned earlier, and is also why spiral galaxy suddenly turns from rich and beautiful at 6D to blocky and ugly at 7D.
At t=2, t=4, past 5D or so, the state is exactly the same for all dimensions for any initial condition I have tried! We could easily find t=4 for 100D or even 200D: they’re identical!
A lot of xy cells share identical coset stacks…more on that later!
Not only is it kinda pretty (in my humble opinion), it also demonstrates that this whole ordeal is really “just a multivalued 2D cellular automaton”: it’s like a “multi-valued” Game of Life, where instead of cells being on and off, they are one of several discrete choices of values. Instead of a “binary” game of life with a boolean at each cell, it’s an “integer” game of life with a finite choice at each cell.
Because there are \({ {\hat{d}}+t} \choose t\) slice cosets for a given dimension and time, it means that our game is a \(2^{ { \hat{d} + t} \choose t }\)-valued game of life, where each cell can be one of that many options (each slice coset and be present or not). That means at 2D (\(\hat{d} = 0\)), we have a normal 2-valued game of life (\(2^1\)), at 3D we have \(7 \choose 6\) or 7 possible points at t=6, so that’s a \(2^7\) or 128-valued game of life, at 4D we have \(8 \choose 6\) or 28 possible points at t=6, and so that’s a \(2^{28}\) or 268,435,456-valued game of life.
You can see this demonstrated in the simulation above, as well. As you progress, each 2D cell “spreads” to its neighbors according to some complex rule; it’s like watching 2d cells interact with each other in complex ways, without ever even having to think of higher dimensions.
Implementing things this way (and taking advantage of the fact that coset stacks are usually very sparse and have few members) gave a nice conceptual shake-up. But there’s one final thing that this view would unlock that would make the biggest difference.
Repeated Stacks
You might have noticed in the final 10D simulation, if you mouse over an xy cell, it’ll also highlight over all of the other xy cells that hold the same coset stack. For most initial starting positions, you might notice something maybe even more curious — a lot of those stacks are duplicated over many xy cells.
In my personal puzzle input (click to load into the simulation), most of the stacks were duplicated many times across different xy cells. If you highlight the cells in any arbitrary starting condition through t=6, you’ll see too that many (if not most) xy cells have multiple other xy cells that have identical stacks to them.
This final insight yields the final optimization we have discovered, as of time of writing. We can actually treat an entire stack as an “action” that is spread to the xy neighbors: The stack under <x,y>=<3,4> is spread to all its eight 2D neighbors identically (and to itself, too, in a way that excludes the original stack itself). That means if you have a stack, you can compute the contribution to a neighbor (expensive) it has one time, and then repeat that same contribution to every occurrence of a stack. So if a stack is repeated ten times over ten different xy stacks, you only need to compute it once and propagate it to all 9x10 neighbors of those stacks (nine neighbors, including self, times each of the 10 repetitions), for a savings of x90! This can be done by storing map of stacks to contributions as a cache.
def step_with_stack_cache(stacks):
neighbs = {}
stack_cache = {}
for pt_2d, pt_stack in stacks.items():
# get what to place in the same xy cell, and what to place in neighbor
# xy cells
if pt_stack in stack_cache:
# get it from the cache if it exists
(rev_neighbs, rev_neighbs_incl_self) = stack_cache[pt_stack]
else:
# otherwise, build it and store it in the cache
rev_neighbs = Counter()
for pt_nd in pt_stack:
rev_neighbs += Counter(reverse_neighbs(pt_nd))
rev_neighbs_incl_self = rev_neighbs + Counter(pt_stack)
stack_cache[pt_stack] = (rev_neighbs, rev_neighbs_incl_self)
# the actual propagation
# 1. add in the same stack; don't include self
if pt_2d in neighbs:
neighbs[pt_2d] += rev_neighbs
else:
neighbs[pt_2d] = rev_neighbs
# 2. add to nieghboring stacks; include self
for ngb_2 in mk_neighbs(pt_2d)[1:]:
if ngb_2 in neighbs:
neighbs[ngb_2] += rev_neighbs_incl_self
else:
neighbs[ngb_2] = rev_neighbs_incl_self
def validate(pt_2d, pt_nd, ncount):
if pt_2d in stacks and pt_nd in stacks[pt_2d]:
return ncount == 2 or ncount == 3
else:
return ncount == 3
return {pt_2d: frozenset(
pt_nd for pt_nd, n in pt_counts.items()
if validate(pt_2d, pt_nd, n)
)
for pt_2d, pt_counts in neighbs
}With this final piece of the puzzle, I was able to reach 18D 3 seconds in my Haskell solution, and 30D in 5 minutes! Michal Marsalek was also able to build this into their fast Nim solver to reach 40D in 8 minutes, 50D in 32 minutes, 60D in 120 minutes.
And as far as I know, this seems to be where things stand today (Feburary 2021).
Conclusions
Hope you enjoyed this journey! My hope is that I was able to convey a fraction of the excitement, wonder, and mystery I felt during the process. At every point, we had no reason to believe something better would come around the corner, but we held on to a hope and faith that kept on rewarding us.
Visualization and different perspectives seem to drive almost every revelation — from the visually striking symmetries of the 3D and 4D simulations, the explorations of how neighbor relationships work, the insight that we could treat the entire problem as a fancy multivalued 2D game of life…all of it came about from being able to see the problem visually in different ways. At other times it was a simple change in perspective to find a better way of encoding variants or looking at how a specific number changed. I know for myself, the next time I try to explore something like this, I will try to apply what I learned to always reach for visualization sooner. Even dead-end visualizations can sometimes provide a new depth to the puzzle that you might appreciate later on.
Another thing I hope was apparent was the power of community! I know I definitely would not have had as much fun doing this if it wasn’t for the vibrant Advent of Code “Ante-Pushing” community. What I’ve described is just one story (Day 17, 2020) out of so many that Advent of Code community members routinely explore together (through 25 puzzles each year for five years). Most of these discoveries were fun because we always had somebody to share them with, or a way to encourage each other and strive for a common goal. I’m definitely lucky to be standing on giants as a part of a talented and passionately curious community that’s excited to explore things like this. Michal Marsalek has his own writeup of the discoveres mentioned here, that you should check out too if you have the time!
Thank you to so many people — Michal Marsalek, Peter Tseng, leftylink, sim642, ephemient, yitz, cyphase, phaazon, glguy, /u/cetttbycettt, /u/bsterc, /u/flwyd, and so many others that I probably missed. An especially deep thanks to Eric Wastl for hosting a wonderful event like Advent of Code every year. Finally, a profoundly deep thanks to the late John Conway, who revealed to us how much joy can come from the exploration of all things mathematical, a genius who was taken away from this world much too soon.
And of course, in making this post, I’m inviting you, the reader, to join us along in this journey as well! It’s hardly over :) Now that you’re up to speed with all of us, I’d be excited to hear about anything you might discover while playing around with this too!
Looking forward at least, there are a some open threads still.
- Notice on the 4D simulation, very soon after simulations start, the two diagonals become very empty, and especially the 3x3 region at the origin where they intersect. It turns out that reflection symmetry boundaries are very inhospitable because they have so many neighbors after reflection, especially at higher dimensions (see the top-right slice at each q level in the 5D symmetries). Could these “dead zones” be extended and exploited at higher dimensions?
- The most promising to me: for t=6, the exact same xy cells are always inhabited for any dimension past 7D or so, and the stacks at each seem to only change slightly from dimension to dimension. If we can analytically find how the stacks at any given position change between 9D and 10D, 10D and 11D, etc., then it will be easy to jump directly to t=6 at 100D without simulating anything. Another way to say this is — can we simulate by fixing t and stepping d, instead of fixing d and stepping t?
Who can tell how far we can go? Michal has a personal goal that I would also be very happy to reach:
I won’t be satisfied until I implement a solution that runs in polynomial time in both t and d.
— Michal Marsalek
Will you, dear reader, be the one to take us there? :)
Special Thanks
I am very humbled to be supported by an amazing community, who make it possible for me to devote time to researching and writing these posts. Very special thanks to my supporter at the “Amazing” level on patreon, Josh Vera! :)
And…there’s actually a neat optimization we can use (brought to our attention by Peter Tseng) to avoid the check of the original set in step 2c above: when you iterate over each point, increment the eight neighbors’ map values by 2, and then increment the point itself by 1. Then in the final integer under each key,
n / 2orn >> 1gives you the number of neighbors andn % 2(modulus) gives you whether or not that cell was alive.↩︎There’s another optimization too you could use that would allow you to ignore this and just treat a cell as its own neighbor; you’d have to tweak the live-or-dead rules slightly, but it does simplify a lot of the propagation logic.↩︎
For dramatic effect, I’ve omitted the fact that while there are only 3003 possible higher-dimensional points, there are \(20^2 \times 3003\) actual unique points possible factoring in the 20x20 x-y grid. Still, it’s a pretty big improvement over the original situation (\(20^2 \times 815730721\)).↩︎
It’s also interesting to note that above 9D (where there are 7 higher-dimensional coordinates), there is always at least one duplicated number. Although I don’t really know a way to explicitly exploit that fact even now, it does mean that there’s a qualitative difference between 9D and below and 10D and above: anything above 9D is…especially degenerate.↩︎
One useful lasting thing I did find (that I won’t spend too much time on here) was a way to index into an enumeration of all of the slice cosets (that is, all the normalized higher-dimensional coordinates). I no longer store
<z,w,...>points as vectors, but rather as a single integer representing their index in that enumeration, which is easier to access and store. I also found a way to do streaming decoding and encoding between that index and the components it represents, allowing me to stream neighbor weights in constant time. This dense index encoding was actually really useful in implementing the Javascript demos on this page :)↩︎